Question

How to graph a parabola $y = - 3{\left( {x - 2} \right)^2} + 5$?

Answer 1

Here, we will compare the given equation with the general equation of parabola to find the vertex. Then we will find $x$ and $y$ intercepts and also an additional point by substituting different values of the variables in the vertex form of the given equation. Using this we will plot those points on a graph and join them together to find the required graph of the given parabola.

Complete step by step solution:
The given quadratic equation in vertex form is $y = - 3{\left( {x - 2} \right)^2} + 5$
Comparing this with $y = a{\left( {x - h} \right)^2} + k$, where $a$ is the axis of symmetry and $\left( {h,k} \right)$ is the vertex.
Now, in order to graph a parabola of this quadratic equation, first of all, we will find the vertex.
Now, since, according to the question, $a = - 3 < 0$ therefore, the vertex will be at the maximum point and the parabola will open downwards.
Thus, comparing the given equation with the general equation, we have,
Vertex $\left( {h,k} \right) = \left( {2,5} \right)$
Now, substituting $x = 0$ in the given quadratic equation $y = - 3{\left( {x - 2} \right)^2} + 5$, we get,
$y = - 3{\left( {0 - 2} \right)^2} + 5$
$\Rightarrow y = - 3 \times 4 + 5 = - 12 + 5 = - 7$
Hence, when $x = 0$, $y = - 7$.
Therefore, the $y$-intercept is $\left( {0, - 7} \right)$
Similarly, substituting $y = 0$ in the given quadratic equation $y = - 3{\left( {x - 2} \right)^2} + 5$, we get,
$0 = - 3{\left( {x - 2} \right)^2} + 5$
$\Rightarrow 3{\left( {x - 2} \right)^2} = 5$
Dividing both sides by 3, we get
$\Rightarrow {\left( {x - 2} \right)^2} = \dfrac{5}{3}$
Taking square root on both sides, we gt
$\Rightarrow x - 2 = \pm \sqrt {\dfrac{5}{3}}$
Adding 2 on both sides, we get,
$\Rightarrow x = 2 \pm \dfrac{{\sqrt 5 }}{{\sqrt 3 }}$
Hence, when $y = 0$, $x = 2 + \dfrac{{\sqrt 5 }}{{\sqrt 3 }},2 - \dfrac{{\sqrt 5 }}{{\sqrt 3 }}$
Therefore, the $x$-intercepts are $\left( {2 + \dfrac{{\sqrt 5 }}{{\sqrt 3 }},0} \right)$ and $\left( {2 - \dfrac{{\sqrt 5 }}{{\sqrt 3 }},0} \right)$
If we do the approximate then, the $x$-intercepts are $\left( { \approx 3.291,0} \right)$ and $\left( {0.709,0} \right)$
Now, we will find an additional point also.
Thus, let $x = 4$
Hence, we get,
$y = - 3{\left( {4 - 2} \right)^2} + 5$
$\Rightarrow y = - 3 \times 4 + 5 = - 12 + 5 = - 7$
Hence, additional point is $\left( {4, - 7} \right)$
Now, we will draw the graph of parabola, such that,
Its vertex is $\left( {2,5} \right)$
The $x$-intercepts are $\left( { \approx 3.291,0} \right)$ and $\left( {0.709,0} \right)$
The $y$-intercept is $\left( {0, - 7} \right)$
An additional point is $\left( {4, - 7} \right)$
Hence, the required graph is:

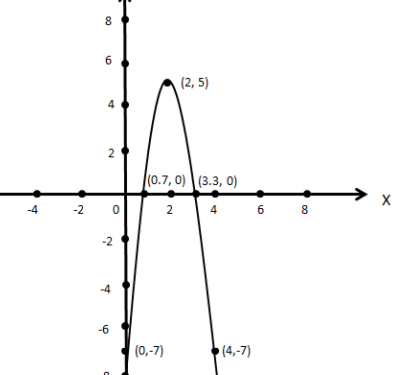
Hence, this is the required answer.

Note:
A parabola is a curve having a focus and a directrix, such that each point on parabola is at equal distance from them. The axis of symmetry of a parabola is a line about which the parabola is symmetrical. When the parabola is vertical, the line of symmetry is vertical. When a quadratic function is graphed in the coordinate plane, the resulting parabola and corresponding axis of symmetry are vertical.