Question
Question: How to get the surface area of a cone using integral calculus \[?\]...
How to get the surface area of a cone using integral calculus ?
Solution
This question describes the operation of finding the area of a circle and lateral surface of the cone. We need to know the basic integration and differentiation. Also, we need to know the process of findingsinθ, cosθand tanθfrom the triangle.
We need to know trigonometric conditions to make an easy calculation.
Complete step by step solution:
In the given question we have to find the total surface area of a cone using integral calculus. For finding the surface area the following figure will help us,
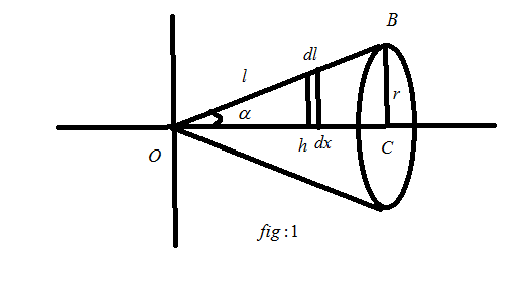
In the above figure,
C is the center of the bottom of the cone,
lis the length of slant edge in the cone,
his the vertical height of the cone,
α is the angle between OCand OB,
dl is the small part of the slant edge,
dx is the small part of vertical height,
ris the radius of the bottom cone.
We know that the bottom of the cone is a circle. So, we have to find the area of the circle. For finding the area of the circle we assume the following figure,
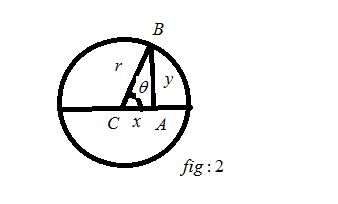
The above figure was drawn with the reference offig:1. From thefig:2, we get the following equation
x2+y2=r2→(1) (By Pythagoras theorem)
The above equation can also be written as
y2=r2−x2
y=r2−x2
The area of the circle,
Acircle=∫r2−x2dx
Let’s taker2it as a common term, so we get
Acircle=∫r2(1−r2x2)dx
We know thatr2=r
Acircle=r∫(1−r2x2)dx→(2)
If we consider the limit between−randr we can evaluate the area of half of the circle.
Fromfig:2we get the following values,
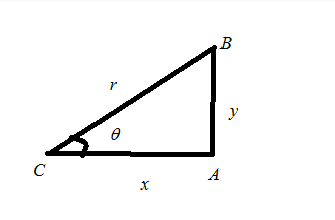
θ=arcCos(rx)
Let’s takex=−r
θ=arcCos(r−r)
θ=arcCos(−1)
We know that, arcCos(−1)=π
So, θ=π
Let’s take x=r
θ=arcCos(rr)
θ=arcCos(1)
We know that, arcCos(1)=0
So, θ=0
We know that,
cosθ=rx
Let’s differentiate the above equation, we get
−sinθdθ=r1dx
So, we get
So, the equation(2)is,
Acircle=r∫(1−r2x2)dx
(For finding the area of half of the circle the limit will beπto0.)
Let’s substitute r2x2=1−sin2θ,dx=−rsinθdθin the above equation, we get
21Acircle=rπ∫01−(1−sin2θ)(−rsinθdθ) 21Acircle=rπ∫01−1+sin2θ(−rsinθdθ)Here, ris constant, so it can be taken to the outside of the interval.
)$$ $$\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\sin \theta .\sin \theta d\theta } $$ $$\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {{{\sin }^2}\theta d\theta } $$ We know that, $${\sin ^2}\theta = \dfrac{{1 - \cos 2\theta }}{2}$$. So, we get $$\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\dfrac{{1 - \cos 2\theta }}{2}d\theta } = - {r^2}\int\limits_\pi ^0 {\left( {\dfrac{1}{2} - \dfrac{{\cos 2\theta }}{2}} \right)d\theta } $$ From equation$$\left( 1 \right)$$ $${x^2} + {y^2} = {r^2} \to \left( 3 \right)$$ Let’s differentiate the above equation, we get $$2xdx + 2ydy = 2rdr$$ In the above equation$$r$$is constant so, $$dr = 0$$. So, the above equation becomes, $$2xdx + 2ydy = 0$$2xdx = - 2ydy \\
\dfrac{{dy}}{{dx}} = \dfrac{{ - 2x}}{{2y}} = \dfrac{{ - x}}{y} \to \left( 4 \right) \\
{y^2} = {r^2} - {x^2} \\
y = \sqrt {{r^2} - {x^2}} \\
ds = \sqrt {1 + {{\left( {\dfrac{{ - x}}{{\sqrt {{r^2} - {x^2}} }}} \right)}^2}} dx \\
ds = \sqrt {1 + \dfrac{{{x^2}}}{{{r^2} - {x^2}}}} dx \\
ds = \sqrt {\dfrac{{{r^2} - {x^2} + {x^2}}}{{{r^2} - {x^2}}}} dx \\
ds = \sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} dx \\
Half of the circumference of the circle is given below, $$L = \int\limits_{ - r}^r {ds} $$ By substituting the value of$$ds$$ we get, $$L = \int\limits_{ - r}^r {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } dx$$ We know that, $$x = r\cos \theta $$, $$dx = - r\sin \theta d\theta $$so, the above equation becomes $$L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } \left( { - r\sin \theta } \right)d\thetaL=π∫0r2−(rcosθ)2r2(−rsinθ)dθ
L=π∫0r2(1−cos2θ)r2(−rsinθ)dθ
We know that, 1−cos2θ=sin2θso, the above equation become,
L=π∫0r2(sin2θ)r2(−rsinθ)dθ
L=−rπ∫0sinθ1.sinθdθ
L=−rπ∫01dθ
So, the full circumference of the circle is2L=2πr
So, the lateral surface area of the cone
S=0∫h2πf(x)dl
Here,y=f(x)
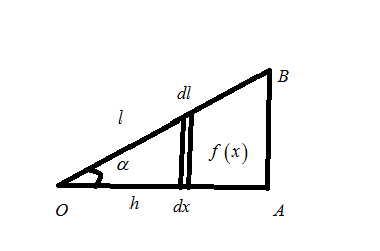
From the given figure
cosα=lh l=cosαh dl=cosαdh=cosαdx tanα=hr=xf(x)f(x)=xtanα
By using the above values we get,
S=0∫h2πxtanαcosαdx
S=2πcosαtanα0∫hxdx
S=2π(lh)(hr)[2x2]0h S=2π(h2rl)[2h2−202] S=2πrSo, the total surface area of the cone=total surface area of the circle+total surface area of the lateral surface.
The total surface area of the cone=πr2+2πr
Note: We have to consider the bottom of the cone as a circle. At first, we want to find the area of a circle, and next, we want to find the area of the lateral surface. Also, note that the integral of cosθissinθ and the differentiation of cosθis−sinθ. If a constant term is present inside the integral, we can take the term outside of the integral.
