Question

How to find the volume of a sphere using integration?

Answer 1

We will draw a rough figure representing a sphere. We will consider a disc of a certain radius about the y-axis. Then we will find the value of the radius in terms of its height from the centre of the sphere and the radius of the sphere. We will integrate the area of this disc along the y-axis where the limits for integration will be the points where the height of the sphere is maximum and minimum.

Complete step-by-step solution:
The rough diagram of the sphere looks like the following,

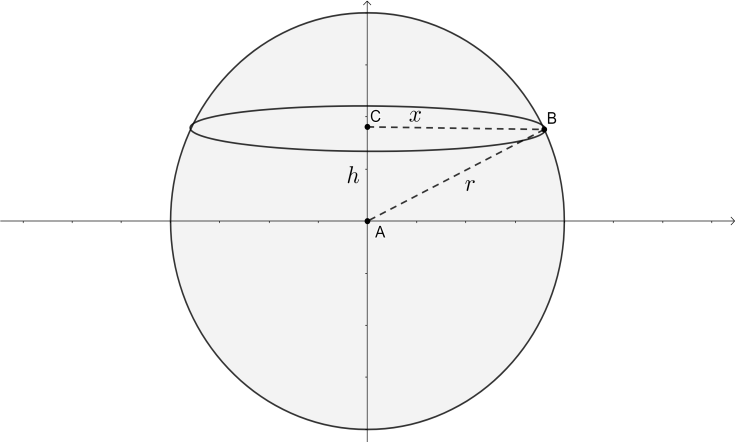
We have to find the volume of this sphere using integration. We have a sphere centered at the origin with radius $r$. Let us consider a disc about the y-axis at a height $h$ and having radius as $x$. The radius of the disc is $x$. Now, from the figure, we can see that $\Delta ACB$ is a right angled triangle with the hypotenuse AB. So, using the Pythagoras theorem in this triangle, we get the following,
$\begin{aligned} & A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}} \\\ & \Rightarrow {{r}^{2}}={{h}^{2}}+{{x}^{2}} \\\ & \Rightarrow {{x}^{2}}={{r}^{2}}-{{h}^{2}} \\\ & \therefore x=\sqrt{{{r}^{2}}-{{h}^{2}}} \\\ \end{aligned}$
The area of this disc is ${{A}_{Disc}}=\pi {{x}^{2}}$. Substituting the value of $x$ in this formula, we get
${{A}_{Disc}}=\pi \left( {{r}^{2}}-{{h}^{2}} \right)$
The discs from the lowest height of the sphere to the highest height of the sphere will fill up the sphere. So, we can calculate the volume of the sphere by integrating the areas of the discs from the lowest height of the sphere to the highest height of the sphere. The lowest height is $-r$ and the highest height of the sphere is $r$. So, we have the following integral,
${{V}_{sphere}}=\int\limits_{-r}^{r}{\pi \left( {{r}^{2}}-{{h}^{2}} \right)dh}$
Integrating the above expression, we get
${{V}_{sphere}}=\left. \pi \left( h{{r}^{2}}-\dfrac{{{h}^{3}}}{3} \right) \right|_{-r}^{r}$
Substituting the limits, we get the following,
${{V}_{sphere}}=\pi \left( r\cdot {{r}^{2}}-\dfrac{{{r}^{3}}}{3} \right)-\pi \left( -r\cdot {{r}^{2}}-\dfrac{{{\left( -r \right)}^{3}}}{3} \right)$
Simplifying the above equation, we get

& {{V}_{sphere}}=\pi \left( \dfrac{2{{r}^{3}}}{3} \right)-\pi \left( -\dfrac{2{{r}^{3}}}{3} \right) \\\ & \Rightarrow {{V}_{sphere}}=\pi \left( \dfrac{2{{r}^{3}}}{3}-\left( -\dfrac{2{{r}^{3}}}{3} \right) \right) \\\ & \therefore {{V}_{sphere}}=\dfrac{4\pi {{r}^{3}}}{3} \\\ \end{aligned}$$ Thus, we have derived the formula for the volume of the sphere. **Note:** The infinitesimal we used in the integration is $dh$ because we are integrating from the lowest height of the sphere to the highest height of the sphere. We can use the y-coordinate instead of the height variable. We should be careful with the signs while opening the brackets, so that we can avoid making errors in the calculations.