Question

How to find the value of ‘$\cos ec{210^ \circ }$’ ?

Answer 1

Hint : Here, we will be going to use the most eccentric concept of ‘trigonometry’. So, to find out the desired value, first of all extract the given angle that it will get the standard angle such as ${0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ },{180^ \circ },{270^ \circ },{360^ \circ }$, etc. Hence, using the rules of trigonometric angles with respect to the various quadrants i.e. I, II, III, IV respectively. As a result, substituting the value for the respective ratio (from the trigonometric table), the required value is obtained.

Complete step-by-step answer :
Since, we have given that
$\cos ec{210^ \circ }$
As a result,
To find the desired value,
First of all, splitting up the given angle ‘${210^ \circ }$’, so that the standard angle is obtained that is
$\Rightarrow \cos ec{210^ \circ } = \cos ec\left( {{{180}^ \circ } + {{30}^ \circ }} \right)$
Hence,
We know that, angle ‘${270^ \circ }$’ lies in III quadrant, which exists that the given trigonometric ratio remains the same (or, as it is) and the given angle (or, ratio) ‘$\theta$’ is/must be positive only in case of ‘$\tan \theta$’ & ‘$\cot \theta$’ and negative for all remaining ratios/angles that is ‘$\sin \theta$’, ‘$\cos \theta$’, ‘$\sec \theta$’, ‘$\cos ec\theta$’, which in term knows as “supplementary angle for trigonometric ratios”.
Hence, we get,
$\Rightarrow \cos ec{210^ \circ } = \cos ec\left( { - {{30}^ \circ }} \right)$
$\Rightarrow \cos ec{210^ \circ } = - \cos ec{30^ \circ }$
Substituting the value of ’ $\cos ec{30^ \circ } = 2$
So, the correct answer is “-2”.

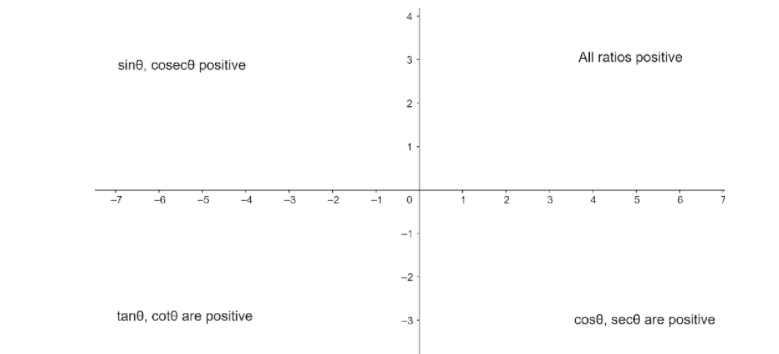
Note : Whenever we come up with this type of problem, always remember the rule for considering the ‘sign’ of the angle, say, ‘$\theta$’ and the change in the respective ratio of the desired expression, which varies within different quadrants. Refer, the below figure to consider the sign as well as the ratio such that “first quadrant” has exists positive angle for all the trigonometric ratios with the changes in the respective ratio like ‘sine’ changes to ‘cosine’, ‘tangent’ to ‘cotangent’, ‘secant’ to ‘cosecant’ and vice versa; in “second quadrant” only ‘sine’ and its inverse ‘cosecant’ is positive with same respective ratios i.e. ‘sine’ remains ‘sine’ and so on; “third quadrant” has ‘tangent’ and ‘cotangent’ positive with the change in the certain respective ratios; and in “fourth quadrant” only ‘secant’ and ‘cosecant’ is positive by keeping the ratios as it is