Question

How to find the static friction between stacked blocks so that the top block does not slip when the bottom block is accelerated?

Answer 1

To solve this problem we will apply a force of F newton on lower block and by balancing net force we will calculate frictional force acting on the upper block. Later on we will discuss the slippery conditions of upper block or minimum static friction needed to oppose the motion of upper block.
Formula used:
$F=m\cdot a$
$N=m\cdot g$
${{F}_{s}}=\mu N$

Complete answer:
Let us assume that the force of F newton acting on the lower block causes a motion on a frictionless surface but there is a static friction between the blocks.

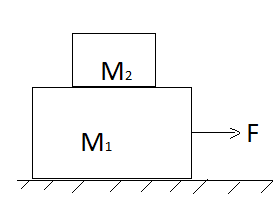
Now, first we need to consider all the vertical and horizontal forces acting on both the blocks which are represented in below diagram,

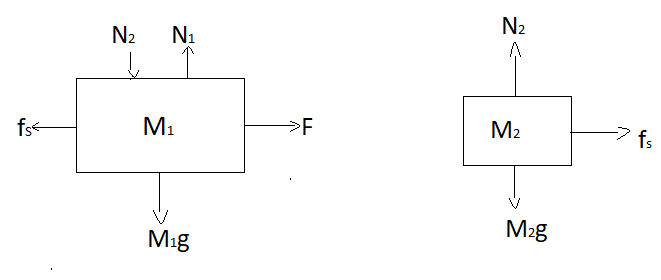
We know that there is no force acting on the upper block but the body is in rest. When a force applied to lower block, due to inertia of rest upper block will try to remains at rest so it will try to move backward with respect to lower block but, due to opposite frictional force acted upon it will move along with the larger block so frictional force will act towards right and for the lower block it will be in opposite direction towards left. Now bye balancing net forces on both the blocks we have,
$=>F-{{f}_{s}}={{M}_{1}}a$
$=>{{f}_{s}}=\mu {{N}_{2}}={{M}_{2}}a$
Here, F(Force applied on larger block), ${{f}_{s}}$(frictional force), ${{N}_{2}}$(normal reaction), a (acceleration of blocks), $\mu$(coefficient of static friction).
$=>{{N}_{2}}={{M}_{2}}g$ so,
$=>{{f}_{s}}=\mu {{M}_{2}}g$
By above equations for upper block we have,
$=>\mu {{M}_{2}}g={{M}_{2}}a$
$=>a=\mu g$
For lower block,
$=>F={{M}_{1}}a+{{f}_{s}}={{M}_{1}}\mu g+\mu {{M}_{2}}g$
(From the value of acceleration calculated above)
$=>F=\mu g({{M}_{1}}+{{M}_{2}})$
$=>\mu =\dfrac{F}{g({{M}_{1}}+{{M}_{2}})}$
$\therefore$ The minimum static frictional force so the upper block will not slip is given by
$=>{{f}_{s}}=\mu {{M}_{2}}g$
And the value of coefficient of friction will be,
$=>\mu =\dfrac{F}{g({{M}_{1}}+{{M}_{2}})}$

Note:
Inertia of rest plays a significant role in providing necessary frictional force between the blocks which provides forward frictional force for the upper block to move and backward for the lower block to oppose its state of motion. When the force applied to the lower block exceeds the value,
$F=\mu g({{M}_{1}}+{{M}_{2}})$
The upper block will slip from the surface and the static frictional force will convert into kinetic friction.