Question

How to find the maximum distance traveled by a ball of mass M, tied to a light elastic string, projected vertically downwards with an initial velocity of ${{V}_{0}}$
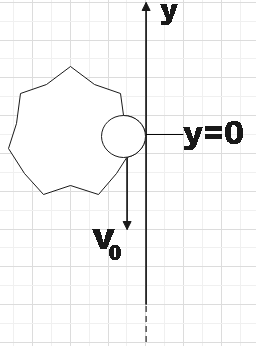
A particle of mass m is attached to one end of a light elastic string of force constant k and unstretched length of${{l}_{0}}$. The other end of the string is fixed onto a vertical frictionless wall at y=0 as shown in the figure. The particle is then projected vertically downwards from the position y=0 with a velocity ${{v}_{0}}$ $\left( {{v}_{0}}\langle \sqrt{2g{{l}_{0}}} \right)$ . Neglect the air resistance. After passing through its lowest point in the path, the particle will again come to rest momentarily at a point whose y coordinate is

A. $-\dfrac{\left[ m\left( {{v}_{0}}^{2}+2g{{l}_{0}} \right)-k{{l}_{0}}^{2} \right]}{2gm}$
B. $-\dfrac{\left( {{v}_{0}}^{2}+2g{{l}_{0}} \right)}{2g}$
C. $\dfrac{{{v}_{0}}^{2}+2g{{l}_{0}}}{2g}$
D. $\dfrac{m{{v}_{0}}^{2}+k{{l}_{0}}^{2}}{gm}$
E. $\dfrac{{{v}_{0}}^{2}}{2g}$

Answer 1

As a first step, you could note down the points given in the question that seem important. You could then think of the consequences of these points on the given situation. Then, you could simply use the law of conservation of energy to begin with solving the given problem.

Complete answer:
In the question, we are told that the ball rises from the lowest point crosses y=0 and is moving upwards. We also know that at the highest most this ball is coming to rest. In the figure we see this point to be y. Now by using the law of conservation of energy we have the sum of the mechanical potential energy of the string and gravitational potential energy to be equal to the initial kinetic energy. That is,
$Mech.P.E+mgy=\dfrac{1}{2}m{{v}_{0}}^{2}$
We are given in the question that,
${{v}_{0}}\langle \sqrt{2{{l}_{0}}g}$
$\Rightarrow initial.K.E=\dfrac{1}{2}m{{v}_{0}}^{2}\langle \dfrac{1}{2}m\times 2{{l}_{0}}g$
$\Rightarrow initial.K.E\langle mg{{l}_{0}}$
That is, we could say that the initial kinetic energy is not sufficient enough to raise the ball from the mean position y=0 to its unstretched length ${{l}_{0}}$ on its way up.
The mechanical Potential energy would remain zero until the string remains slack. So, we could make the conclusion that,
$mgy=\dfrac{1}{2}m{{v}_{0}}^{2}$
$\therefore y=\dfrac{{{v}_{0}}^{2}}{2g}$
Therefore, we found the y coordinate to be, $y=\dfrac{{{v}_{0}}^{2}}{2g}$.

Hence, option E is the correct answer.

Note:
This question seems like the best example for every minute detail given in the question becoming a significant point in solving the question. You may have noted that the whole solution above is expanded by using the minute inequality relation in the question along with the help of law of conservation of energy.