Question

How to find the horizontal distance of a projectile in a projectile motion?

Answer 1

Begin by resolving the initial velocity, acceleration and displacement vectors into their corresponding horizontal and vertical components. Use the kinematic equation of motion relating displacement, initial velocity, time of flight and acceleration due to gravity to arrive at appropriate expressions that can be solved and rearranged to arrive at the necessary equation for the horizontal distance. Remember to account for all components of the above quantities and define their relevance in a given direction carefully.

Formula Used:
Horizontal distance: $s_x = \dfrac{u^2sin2\theta}{g}$

Complete Solution:
Let us deconstruct the question to understand it in terms that are familiar to us.
The question basically deals with a case of projectile motion. Projectile motion is a form of motion where an object moves in a parabolic path. It occurs when there is one force that launches the object after which the only influencing force is gravity. The path that the object follows under this influence of gravity is called projectile trajectory. In most cases for our convenience, we neglect air resistance.
The horizontal distance, oftentimes called the range, is the distance that the projectile travels in the horizontal direction. Let us consider a projectile launched from point O at an angle $\theta$ with the x-axis, with a launch velocity $u$.

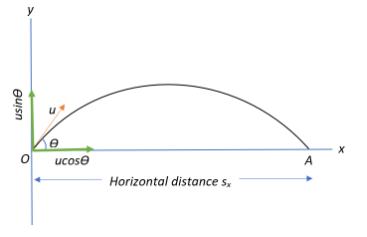
We can resolve the launch velocity into its horizontal and vertical components as:
$u_x = ucos\theta$ and $u_{y} = usin\theta$
The projectile experiences an acceleration due to gravity vertically downwards, therefore, we have:
$a_x=0$ and $a_y =-g$

Since projectile motion is two dimensional, the displacement of the projectile in horizontal and vertical directions in time t can be given by the kinematic equation of motion(s):
$s_x = u_x t + \dfrac{1}{2}a_xt^2 = ucos\theta.t$, and
$s_y = u_y t + \dfrac{1}{2}a_yt^2 = usin\theta.t -\dfrac{1}{2}gt^2$
Now, we know that, since the particle returns back to the ground at A, the vertical displacement of the particle will be $s_y=0$
$\Rightarrow 0 = usin\theta.t -\dfrac{1}{2}gt^2 \Rightarrow (t)(usin\theta - \dfrac{1}{2}gt) = 0$
This means that either $t=0$ or $t= \dfrac{2usin\theta}{g}$ .
We know that the projectile travels a finite horizontal distance $s_x$, so the correct choice would be $t= \dfrac{2usin\theta}{g}$, since $t=0$ signifies the initial time.
Substituting the value of t in the expression for $s_x$ we get:
$s_x = ucos\theta .t = ucos\theta.\left(\dfrac{2usin\theta}{g}\right) = \dfrac{u^2 2cos\theta sin\theta}{g}$
We use the trigonometric equation $2cos\theta sin\theta = sin2\theta$ and we get:
Horizontal distance: $s_x = \dfrac{u^2sin2\theta}{g}$

Note:
While resolving the vectors into their horizontal and vertical components, remember to assign the sine and cosine values correctly since it is a common misconception that the horizontal side is always the cosine part and the vertical side is the sine part.
The correct way to go about this would be to establish that the component that is adjacent to $\theta$ assumes a cosine value, whereas the component that is opposite to $\theta$ assumes a sine value.
Also, note that though we refer to our result as the horizontal distance, it is essentially the horizontal “displacement” that we calculate. This is also why we took the vertical displacement to be 0 in our problem, because otherwise the projectile has travelled a significant vertical distance.