Question

How to draw the R region of integration and change the order of Integration (do not evaluate the integral)? $\int_0^1 {\int_{ - \sqrt {1 - {y^2}} }^{\sqrt {1 - {y^2}} } {dxdy} }$

Answer 1

Here, we will draw the R region of Integration only by using the limits of Integration and not by evaluating the Integral. Then by using the R region of Integration, we will find the order of integration after reversing. Integration is defined as the summation of all the discrete data.

Complete Step by Step Solution:
We are given an Integral function $\int_0^1 {\int_{ - \sqrt {1 - {y^2}} }^{\sqrt {1 - {y^2}} } {dxdy} }$.
The given Integration limit shows that the region is a unit circle, which gives the underlying relationships as:
${x^2} + {y^2} = 1$
Now, the limits of the Integration of the variables $x$ and $y$ are
$\Rightarrow x = \pm \sqrt {1 - {y^2}}$ and $y = \pm \sqrt {1 - {x^2}}$
But, the given limits of the Integration are:
$- \sqrt {1 - {y^2}} \le x \le \sqrt {1 - {y^2}}$ and $0 \le y \le 1$
We will draw the R Region of Integration for the given limits in the first Quadrant ${Q_1}$ and the second Quadrant ${Q_2}$.

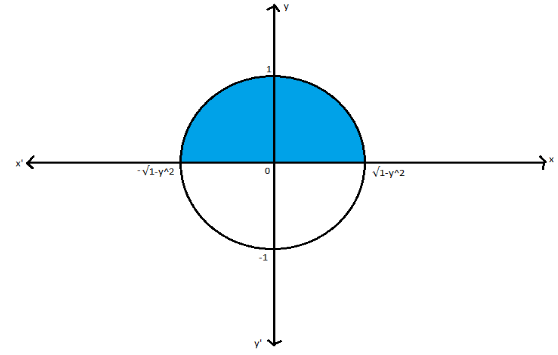
Now, we will change the order of Integration.
$- 1 \le x \le 1$ and $0 \le y \le \sqrt {1 - {x^2}}$
Thus, we will get the Integration after reversing the order of integration as $\int_{ - 1}^1 {\int_0^{\sqrt {1 - {x^2}} } {dydx} }$.
Therefore, the Integration after reversing the order of integration is $\int_0^1 {\int_{ - \sqrt {1 - {y^2}} }^{\sqrt {1 - {y^2}} } {dxdy} } = \int_{ - 1}^1 {\int_0^{\sqrt {1 - {x^2}} } {dydx} }$.

Note:
We know that R region is a region that is common for the given functions and lies in the quadrants. The order of Integration is a process of reversing the order from $dxdy$ to$dydx$. $\int_a^b {f\left( x \right)dx}$ where $a$ is the lower limit of the Integral and $b$ is the upper limit of the Integral. We know that Integration is the process of adding the small parts to find the whole parts. Double Integration is defined as the process of Integration over a two Dimensional area.