Question

How to determine the depth of a water well given the initial velocity, the time and the speed of sound?
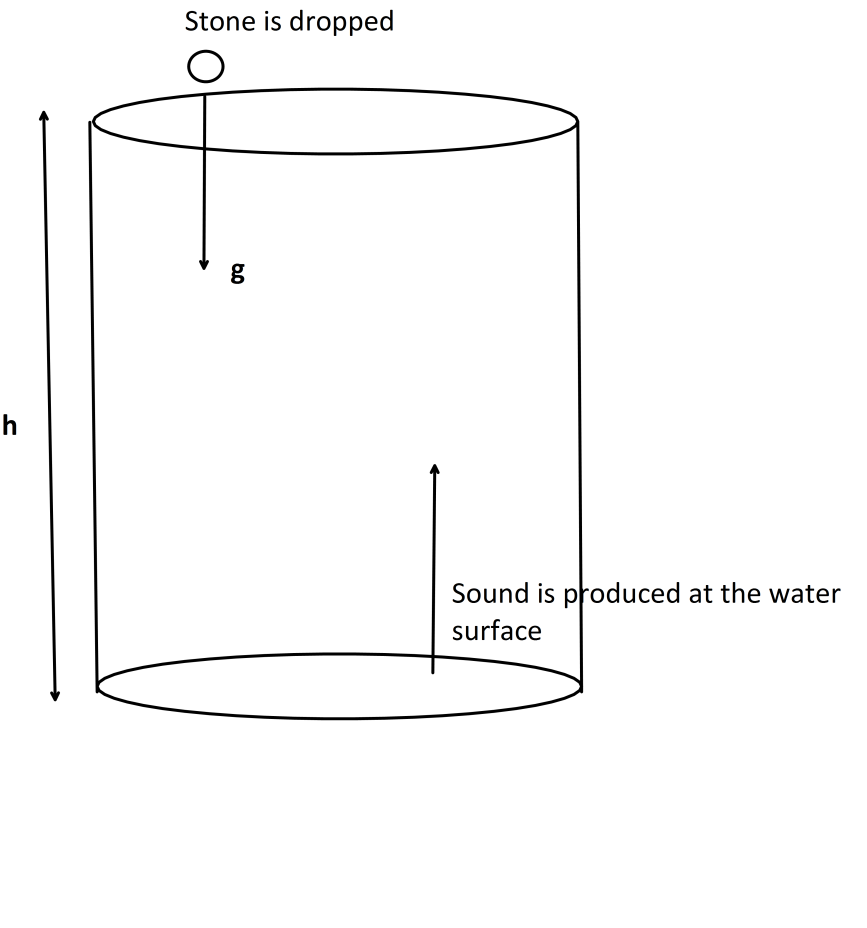
How to determine the depth of a water well, knowing that the time between the initial instant in which a stone is released with zero initial velocity and that in which noise is heard, as a consequence of the impact of the stone on the bottom, is $t = 4.80s$ . Ignore the air resistance and take the sound speed of $340m{s^{ - 1}}$ .

Answer 1

To solve this problem use the equations for rectilinear motion in free fall and calculate the height of the well. For a particle in free fall the height of the particle is given by, $h = ut + \dfrac{1}{2}g{t^2}$ where, $u$ is the initial velocity, $t$ is the time of fall and $g$ is the gravitational acceleration .

Complete step by step answer:
We know if a particle is freely falling under the influence of gravitation the equation of motion is written as, $h = ut + \dfrac{1}{2}g{t^2}$ where, $u$ is the initial velocity, $t$ is the time of fall and $g$ is the gravitational acceleration.
Here, we have given, the stone has no initial velocity, so $u = 0m{s^{ - 1}}$ .
Now, let’s assume the depth of the well is $h$ metre and the time taken to fall the height is ${t_1}$
So, the equation of motion for one dimensional motion can be written as, $h = \dfrac{1}{2}g{t_1}^2$
Now, after the impact (at ${t_1}$ ) the sound travels to the mouth of the well. So, time taken by the sound to travel this distance must be, $(4.8 - {t_1})s$ . Since, total time to hear the event is $4.80s$
Now, we have given the velocity of the sound $v = 340m{s^{ - 1}}$ . So, distance travels by the sound is the same height to the top of the well.

So, distance travelled by the sound wave, $h = v(4.8 - {t_1})$
Or, $h = 340(4.8 - {t_1})$
Now, putting the value of $h$ we have,
$\dfrac{1}{2}g{t_1}^2 = 340(4.8 - {t_1})$
Or, $\dfrac{1}{2}9.8{t_1}^2 = 340(4.8 - {t_1})$
Or, $4.9{t_1}^2 = 1632 - 340{t_1}$
Or, $4.9{t_1}^2 + 340{t_1} - 1632 = 0$
Hence, applying Shreedhar Acharya’s rule we get,
${t_1} = \dfrac{{ - 340 \pm \sqrt {{{340}^2} - 4 \cdot 4.9 \cdot ( - 1632} )}}{{2 \cdot 4.9}}$
Up on simplifying we get,
${t_1} = \dfrac{{ - 340 \pm \sqrt {{{340}^2} + 4 \cdot 4.9 \cdot 1632} }}{{9.8}}$
or, ${t_1} = \dfrac{{ - 340 \pm 384.17}}{{9.8}}$
Taking positive sign we get,
${t_1} = \dfrac{{44.17}}{{9.8}} = 4.507$
Taking negative sign we have,
${t_1} = \dfrac{{ - 724.17}}{{9.8}} = - 73.89$
Since, time cannot be negative. Hence,
Hence, time taken to reach the surface of the water in the well for the stone is $4.507s$
So, time taken by sound to reach the top is $(4.80 - 4.507) = 0.293s$
Hence, depth of the well is $h = 340 \times 0.293 = 99.62m$
So, the depth of the well is $99.62m$ .

Note:
We can also use echo of sound to calculate the depth of the well. If we can distinctly hear the echo of the mother sound then we can easily calculate the depth of the sound well using only $s = vt$ provided the speed of the sound. In this case we would hear the echo after $(0.293 + 0.293) = 0.586s$. So, echo can be easily heard by a normal person here and so depth of the well can be calculated easily.