Question

How to determine height of the cylinder with maximum volume engraved in a sphere with radius $R$ ?

Answer 1

Hint : We have to determine the height of the cylinder with maximum volume engraved in a sphere with radius $R$ , its cross-sectional area and height are restricted by the sphere , we know that volume of a cylinder is given by $V = \pi {r^2}h$ . For maximum volume , $\dfrac{{dV}}{{dh}} = 0$ .

Complete step-by-step answer :
Consider a cylinder, however, is engraved in a sphere, its cross-sectional area and height are restricted by the sphere and when the sphere cut vertically then we get the required cross-section as shown below ,

            ![](https://www.vedantu.com/question-sets/0a51ab92-4895-4076-b399-1b1219549ad88967294104142004652.png)   

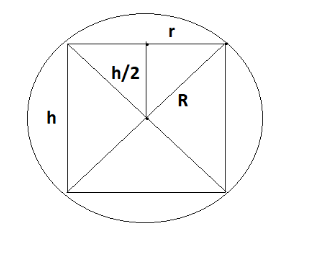
In the above figure ,
‘h’ is the height of the cylinder ,
‘r’ is the radius of the cylinder,
And ‘R’ is the radius of the sphere.
By applying Pythagoras Theorem , we will get the relationship between height of the cylinder, radius of the cylinder, radius of the sphere.
Therefore, we get the following,
$\Rightarrow {R^2} = {\left( {\dfrac{h}{2}} \right)^2} + {r^2}$
Now, simplifying the above equation, we will get ,
$\Rightarrow {R^2} = \dfrac{{{h^2}}}{4} + {r^2}$
For solving radius of the cylinder that is $r$ , we will get ,
$\Rightarrow {r^2} = {R^2} - \dfrac{{{h^2}}}{4}.......(1)$
Volume of a cylinder , $V = \pi {r^2}h$ . (original equation)
Now substitute $(1)$ in our original equation ,
We will get,
$V = \pi {r^2}h$
$= \pi \left( {{R^2} - \dfrac{{{h^2}}}{4}} \right)h$
$= \pi {R^2}h - \dfrac{{{h^3}}}{4} \pi$
For maximum volume , we can write ,
$\Rightarrow \dfrac{{dV}}{{dh}} = 0$
$\Rightarrow \dfrac{d}{{dh}}\left( {\pi {R^2}h - \dfrac{{{h^3}}}{4}}\pi \right) = 0$
$\Rightarrow {R^2} - \dfrac{3}{4}({h^2}) = 0$
We have to solve for height of the cylinder that is $h$ ,
Subtract ${R^2}$ from both the side,

$$\Rightarrow {R^2} - {R^2} - \dfrac{3}{4}({h^2}) = - {R^2} \\\ \Rightarrow - \dfrac{3}{4}{h^2} = - {R^2} \;$$

After simplifying ,
$\Rightarrow \dfrac{3}{4}{h^2} = {R^2}$
Now multiple by $\dfrac{4}{3}$ both the side of the equation, we will get ,
$\Rightarrow {h^2} = \dfrac{4}{3} {R^2}$
Now, taking square root both the side,
$\Rightarrow h = \sqrt {\dfrac{4}{3} } R$
We get the required result.
So, the correct answer is “ $\Rightarrow h = \sqrt {\dfrac{4}{3}} R$ ”.

Note : The important thing to recollect about any equation is that the ‘equals’ sign represents a balance. What the sign says is that what’s on the left-hand side is strictly an equal to what’s on the right-hand side. It is the type of question where only mathematical operations such as addition, subtraction, multiplication and division is used.