Question
Question: How should 5 capacitors each of capacitance \(1\mu F\) be connected so as to produce a total capacit...
How should 5 capacitors each of capacitance 1μF be connected so as to produce a total capacitance of 73μF?
Solution
Capacitors can be connected in combinations in two ways; series and parallel. Select the number of capacitors to be connected in series and the number of capacitors in parallel individually and then connect their equivalent into a combination which gives the required capacitance.
Formula Used:
Ceq1=C11+C21+.......Cn1
Ceq=C1+C2+......Cn
Complete step-by-step solution:
The capacitance of a conductor is its ability to store charge on it. Its SI unit is farad (F).
There are two ways to connect capacitors in combinations; series and parallel combinations
In series combination, the reciprocals of the capacitance get added. The equivalent capacitance is smaller than the smallest value.
Ceq1=C11+C21+.......Cn1
In parallel combination, capacitance gets simply added. The equivalent capacitance is larger than the largest value.
Ceq=C1+C2+......Cn
In order to get an equivalence of 73μF, first we can add two capacitors in series, their equivalence will be-
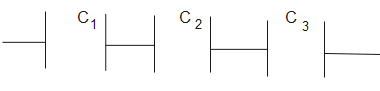
C1=1+1
∴C=21 - (1)
The remaining set of capacitors can be connected in parallel, their equivalence will be-
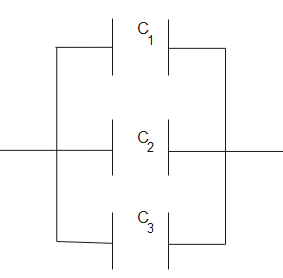
C′=1+1+1
∴C′=3 - (2)
The first set of capacitors connected in series and the second set of capacitors connected in parallel can now be connected in series giving a new equivalent as-
C′′1=211+31⇒C′′1=2+31⇒C′′1=37
∴C′′=73
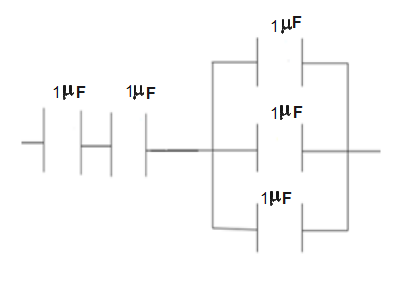
(Each capacitor is of 1μF)
Additional information:
When capacitors are being charged, charge is being stored on their plates and it takes them t=∞ to get charged. When a capacitor is fully charged, the arm in which the capacitor is connected is assumed to have been short-circuited. Half of the total work done by the battery is stored as energy in the capacitor whereas half of it is dissipated as heat.
Note:
Capacitors are devices used to store electrical energy in the presence of an electrical field. Combinations in capacitors are analogous to combinations in resistors. The capacitance of a conductor depends on the permeability of space inside the capacitor, area of cross section and distance between the plates.
