Question
Question: How much work is required to set up the arrangement of the belowfigure if q = 2.30 pC, a = 64.0 cm, ...
How much work is required to set up the arrangement of the belowfigure if q = 2.30 pC, a = 64.0 cm, and the particles are initially infinitely far apart and at rest?
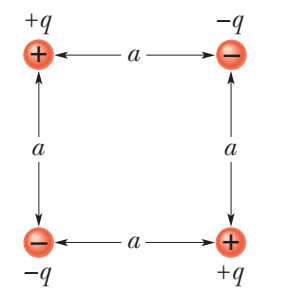
Solution
The work done in bringing charge from an infinity to a certain point needs a maximum amount of potential energy. The work depends on the force between the two charges and the distance between them. This will help you in answering this question.
Complete answer:
In the following diagram, the charges are labelled:
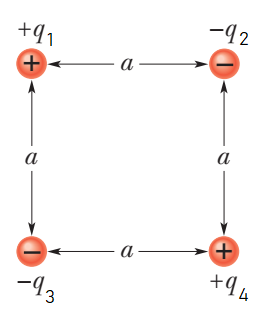
The distance between the charges q1and q4is 2a. Similarly, the distance between the charges q3and q2is 2a.
Thus the work done is the potential energy between the charges.
U1 is the potential energy between the charges q1and q2.
U2 is the potential energy between the charges q1and q3.
U3 is the potential energy between the charges q4and q2.
U4 is the potential energy between the charges q3and q4.
U5 is the potential energy between the charges q1and q4.
U6 is the potential energy between the charges q3and q2.
Here, q1=q2=q3=q4=q5=q6=q
Thus, the total work done is,
W=U1+U2+U3+U4+U5+U6........(i)
U1=U2=U3=U4=a−kq2..........(ii)
Where k=4πε01
U5=U6=a2kq2...........(iii)
From (i), (ii) and (iii), we get,
W=a−kq2+a−kq2+a−kq2+a−kq2+a2kq2+a2kq2W=a−4kq2+a22kq2W=a−4kq2+a2kq2W=akq2(2−4)
By substituting the value, we get,
W=4πε01×(2.30×10−12)2×64×10−21×(2−4)W=−1.92×10−13J
The work done to set up the experiment will be −1.92×10−13J.
Note:
The potential energy depends on the sign of the charge too. Though the value of the work done is negative which is absurd since it is a scalar quantity. The work done comes out to be negative because it is against the electrostatic force.
