Question

How much work is done in ergs in pulling a box $2\,{\text{m}}$ across a tabletop with a force of $20\,{\text{N}}$ in the horizontal direction?

Answer 1

To find the work done in pulling the box across the tabletop, you need to have an expression of work done in terms of displacement and force. Recall such an expression of work done. Put the values of displacement and force in the expression to obtain the work done. Also, the answer is asked in ergs, that is in CGS unit but the displacement and force given are in SI units so you will need to convert your answer to CGS unit.

Complete step by step answer:
Given, displacement of the box is $D = 2{\text{m}}$. Force applied to pull the box in horizontal direction, $F = 20\,{\text{N}}$. To find the work done here, we need to write work done in terms of displacement and force applied. Work done can be defined as the product of component of force in the direction of displacement and the magnitude of displacement that is we can write work done as,
$W = \left( {F\cos \theta } \right)D$ (i)
where $F$is the force applied, $D$ is the displacement and $\theta$ is the angle between force and direction of displacement.

Let us draw a diagram with the given information,

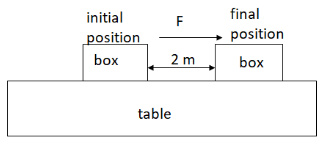
From the diagram we can observe that direction of displacement and force are the same, so angle between force and displacement is ${0^ \circ }$, that is here $\theta = {0^ \circ }$.
Putting the values of $F$, $D$ and $\theta$ in equation (i) we get
$W = \left( {20\cos {0^ \circ }} \right) \times 2$
$\Rightarrow W = 20 \times 2$
$\Rightarrow W = 40{\text{Joules}}$ (ii)
We are asked to calculate the work done in ergs, so we convert joules to ergs.
$1\,{\text{Joule}} = {10^7}{\text{ergs}}$
Using this value in equation (ii) we get,
$\therefore W = 40 \times {10^7}{\text{ergs}}$

Therefore, the required work done in ergs is $40 \times {10^7}{\text{ergs}}$.

Note: Work done can also be written as change in kinetic energy but since here displacement and force were given, so we used the formula for work done in terms of displacement and force applied. Also, remember if the direction of force and displacement are perpendicular to each other then the work done is zero.