Question

How much work does it take to push an object with a mass of $4\;kg$ up a $9\;m$ ramp, if the ramp has an incline of $\dfrac{5\pi}{12}$ and a kinetic friction coefficient of $8$?

Answer 1

We know that work done is defined as the force required displacing an object. Here, since we have an incline, we have to take the component of the incline. We also know that friction is a resistive force acting against the force. Thus taking the above into consideration, we can find the work done.
Formula used:
$W=F.s$

Complete answer:
We know that work done is the energy used to move an object from its position. It is mathematically expressed as follows $W=F.s$
Since both force and displacement are vector quantities, and work is a scalar quantity, we take the dot product or the scalar product of the two to find the work done.
Now consider the inclination as shown below:

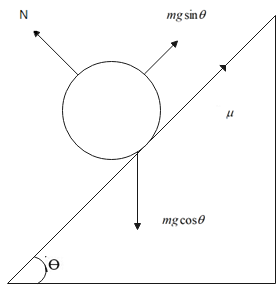
Then the total work done is given as $W=mgh\sin\theta+\mu mgh\cos\theta$ where, $W$ is the work done, $m=4\;kg$ is the mass of the object and the height $h=9m$ due to the inclination $\theta=75^{ \circ}$.Since we have an inclination, we have to take the vector components and to calculate the work done.
We know the conversion between radian and degree as follows,
$1\;rad= \dfrac{180}{\pi}$
Then, converting the given radians into degrees we have
$\implies \dfrac{5\pi}{12}=\dfrac{5\pi}{12}\times \dfrac{180}{\pi}= 75^{\circ}$
Then substituting the values, we have
$\implies W=4\times 10\times 9\times \sin (75)+8\times 4\times 10\times 9\times \cos(75)$
$\implies W= 360(0.965+8\times 0.258)$
$\implies W=360(0.965+2.064)$
$\implies W=360(3.029)$
$\therefore W=1090.34J$

Note:
To calculate the sine and cosine values of the angles, we can also sum of trigonometric angles properties, as $\sin 75= \sin(30+45)$ and similarly, $\cos 75= \cos (30+45)$. Also, here we are converting the angles from radians to degree, for easier calculations. Since we are moving the object from say ground to the top of the ramp, the total distance covered will be the maximum height the object has covered.