Question

How much work did the movers do (horizontally) pushing a $46\,kg$ crate $10.3\,m$ across a rough floor without acceleration, if the effective coefficient of friction was $0.50$?

Answer 1

In such questions we can just draw a free body diagram and balance the forces. By balancing the forces we can get the actual force required to push the object. Once we get the force required to push the object we can easily find the work done.

Formula used:
Work done: $W=F\cdot d$
Where $F$ is the force and $d$ is the displacement.
Frictional force: $f=\mu N$
Where $\mu$ is the friction coefficient and $N$ is the normal force.

Complete step by step answer:
First of all, let us draw a free body diagram for the given situation.

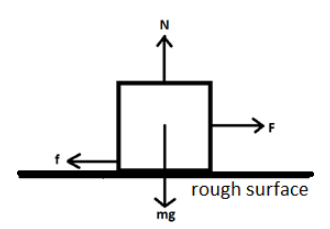
As we can see from the figure, a body of mass $m$ is moving on a rough surface without any acceleration. The surface has a coefficient of friction $f$. Now, we know that the frictional force is given by

\Rightarrow f=\mu mg $$ Where $N$ is the force due to normal and $\mu $ is the friction coefficient. Now, to move the object without acceleration, we need to only outcome the force due to friction. Hence, the force required to move the object is $$F=f \\\ \Rightarrow F=\mu mg $$ From the question, the mass of the object is given as $46\,kg$. The gravitational acceleration is $9.8\dfrac{m}{{{s}^{2}}}$. Therefore, placing the values and solving, we get $$F=(0.50)(46)(9.8) \\\ \therefore F=225.4\,N \\\ $$ **The force required by the pushers to push a crate of $46\,kg$ for a distance of $10.3\,m$ without acceleration, on a rough surface is $225.4\,N$** **Note:** In case force and displacement is perpendicular to each other then, no work will be done whereas if they are in opposite directions negative work is done due to the dot product. . In case the object was pulled upward with the help of string then we also have to consider the tension.