Question

How much space is filled in cubic close packing?

Answer 1

Hint : The 3D Arrangement of different atoms in a row touching each other and forming different layers. When layers containing hexagonal close packing are arranged over each other, two types of arrangement is feasible.

Complete Step By Step Answer:
The third layer is formed in such a way that tetrahedral voids are covered. In this way the spheres of the third layer lie directly above those in the first layer. It means the third layer becomes exactly identical to the first layer. If we consider the first layer as A, and second as B, then this type of packing is ABABAB. arrangement and it is known as hexagonal close packing. Examples are Mg, Zn, Cd, Be etc.
If the third layer is formed in such a way that spheres of the third layer must cover octahedral voids. It forms a new third layer. This is ABCABC… arrangement, and is known as cubic close packing.
To find space occupied: we have the formula of packing efficiency:

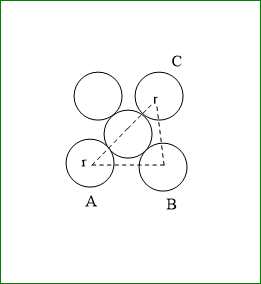
Suppose the edge length of a unit cell is a.
And radius is r
In triangle ABC, $A{C^2} = B{C^2} + A{B^2}$
${a^2} + {a^2} = 2{a^2}$
hence face diagonal $AC = \sqrt 2 a$
but $AC = 4r$
therefore, $4r = \sqrt 2 a$
hence, volume of unit cell = ${a^3} = 16\sqrt 2 {r^3}$
as there are a total of 4 lattice points per unit cell.
Packing efficiency: $= \dfrac{{4 \times \dfrac{{4{\pi ^3}}}{3}}}{{{a^3}or16\sqrt 2 {r^3}}} = \dfrac{{\sqrt 2 \pi }}{6} = 0.74$
Hence, % of space occupied $= 74\%$

Note :
Formation of $3^{rd}$ layer over $2^{nd}$ : there are two types of voids which are to be covered by the third layer. These are octahedral voids which remain occupied for two consecutive layers and tetrahedral voids forming in the second layer.