Question

How many $X - {M^ \wedge } - X\;\left( {90^\circ } \right)\;$ bond angle is/are present in pentagonal bipyramidal geometry?

Answer 1

firstly, we have to draw geometry of the pentagonal bipyramidal, we can do that by knowing the hybridization for that we have to find hybridization and with the corresponding value of z we can make the geometry.

Complete step by step answer:

We can find hybridization by the help of corresponding z value.
${\rm{z}}=\;{\rm{no}}{\rm{.}}\;{\rm{of}}\;\sigma\;{\rm{bond}}\;+\;{\rm{l}}{\rm{.p}}\;{\rm{on}}\;{\rm{central}}\;{\rm{atom}}$

Where, No. of $\sigma$ bond means single bond and l.p is the lone pair present on the central atom.

For value we have to see the following table.

Z	Hybridisation
$2$	$Sp$
$3$	$S{p^2}$
$4$	$S{p^3}$
$5$	$S{p^3}d$
6	$S{p^3}{d^2}$
7	$S{p^3}{d^3}$

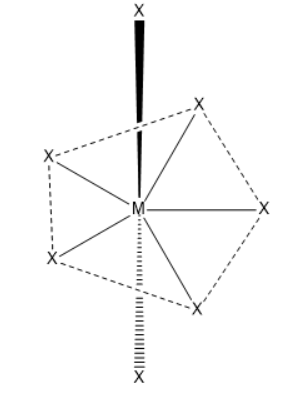
Pentagonal bipyramidal geometry

There will be ten $X - {M^ \wedge } - X\;\left( {90^\circ } \right)\;$ bond angles present in pentagonal bipyramidal geometry.
If we take example of $I{F_7}$ molecule, where $I$ is central atom
By using the above formula we can find its hybridization and we get$z = 7$ which means hybridization will be $S{p^3}{d^3}$.

The mixing of one s, three p and three d atomic orbitals results in the formation of seven equivalent $S{p^3}{d^3}$hybrid orbitals of equal energy. This hybridization is known to be $S{p^3}{d^3}$ hybridization.

Seven atomic orbitals (one s, three p and three d orbitals) will hybridize to form seven $S{p^3}{d^3}$ hybrid orbitals. These are singly filled. These hybrid orbitals overlap with singly filled $2{p_z}$ atomic orbitals of seven F-atoms to form seven I-F sigma bonds. Geometry of$I{F_7}$ is pentagonal bipyramidal and bond angle is $72^\circ$and $90^\circ$.

Properties of $S{p^3}{d^3}$ hybridization
Seven $S{p^3}{d^3}$ hybrid orbitals are directed towards the corners of a pentagonal bipyramidal. These are not equivalent hybrid orbitals because five of them are directed towards the corner of the regular pentagon while the remaining two are directed above and below the plane.

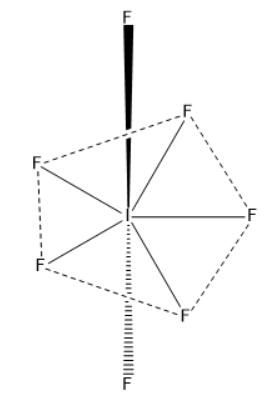
$I{F_7}$
Therefore, there will be ten $X - {M^ \wedge } - X\;\left( {90^\circ } \right)\;$ bond angles present in pentagonal bipyramidal geometry.

Note:
The pentagonal bipyramidal is a molecular geometry which has one atom present at centre and surrounded by seven ligands at the corners of the pentagonal bipyramidal. Coordination no. will be seven. The geometry is pentagonal bipyramidal and angle is $72^\circ$and $90^\circ$.