Question

How many triangles can be formed by joining the vertices of a Hexagon?

Answer 1

To find the number of triangles by joining the vertices of a Hexagon means to find how many three sides figures can be obtained from a six vertices figure and one of the ways to find the same is by the combination ( as in Permutation and Combination) of a number of sides of Hexagon by a number of sides of the triangle.

Formula used:
To find the combination of the number of lesser sided figure from a greater sided figure we use the formula: $C(n,k)=\dfrac{n!}{\left( n-k \right)!k!}$,
where $n$ is the total number of sides of the greater sided figure and $k$ is the total number of sides of the lesser sided figure.

Complete Step-by-step Solution
Placing the values in the formula for $n=6$ which is the greater sided figure or hexagon and for $k=3$ which is the lesser side or triangle we get the combination as:
$C(6,3)=\dfrac{6!}{\left( 6-3 \right)!3!}$
$C(6,3)=\dfrac{6!}{3!3!}$
$C(6,3)=\dfrac{6\times 5\times 4\times 3\times 2\times 1}{3\times 2\times 1\times 3\times 2\times 1}$
$C(6,3)=20$

Hence, the total numbers of triangles formed by joining the vertices of the hexagon are $20$.

Note:
Another method to solve the question is by drawing lines in between the vertices and counting the triangles as such; the process takes a long time to reach the answer but can be helpful in case of not knowing combination and permutation. The figures can be counted as follows:

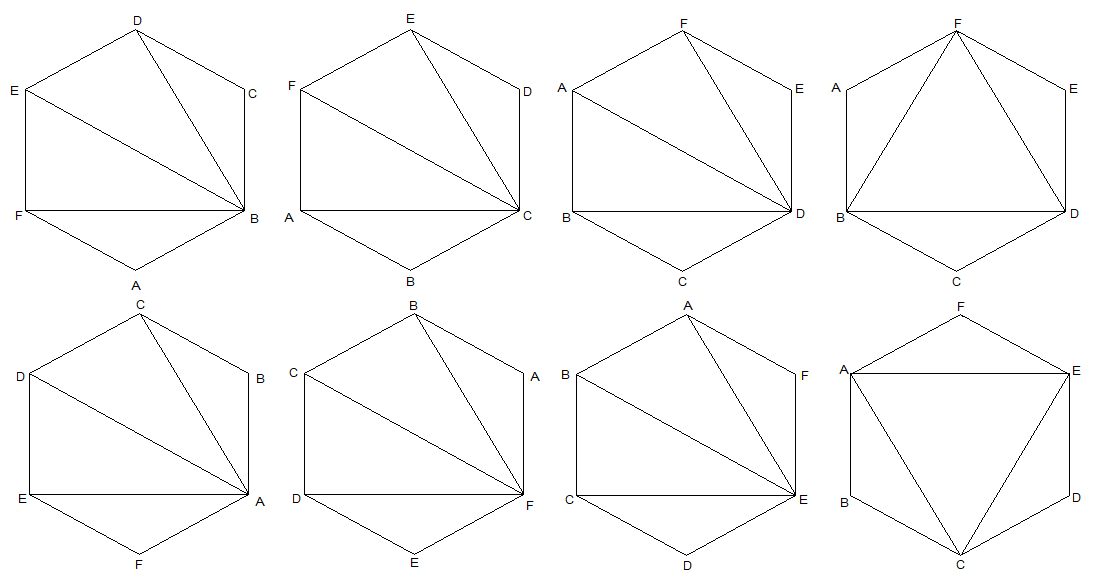
The figures can be calculated in terms of triangles and after eliminating the triangles that have the same terms we get the triangles as:
ACE, ACF, ACD, ACB, AEF, AED, AEB, AFD, AFB, CEF, CED, CEB, CFD, CFB, EFD, EFB, EDB, FBD, ABD, CDB.