Question

How many triangles can be formed by joining the vertices of a hexagon?
A. 31
B. 25
C. 20
D. 60

Answer 1

As we know that hexagon has $6$ vertices means $6$ points and the triangle has $3$ points means a triangle need $3$ vertices to be formed. Then, the numbers of triangles that can be formed by joining the vertices of a hexagon can be calculated by applying the concept of combination.

Complete step by step solution:

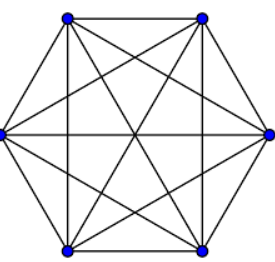
The number of vertices in a hexagon is $6$.
The number of vertices in a triangle is $3$.
That means to make a triangle we need $3$ vertices.
So,$6$is the total number of vertices in hexagons, and out of those 6 vertices, 3 vertices that being chosen at a time to make a triangle.
By applying the formula of combination:
${}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}$ where, n is the total numbers of objects and r is the number of objects to be chosen as a time.
Therefore,
${}^6{C_3} = \dfrac{{6!}}{{3! \times \left( {6 - 3} \right)!}} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}}$
By using the values of factorial terms:
We have, $6!$ can be written as $6 \times 5 \times 4 \times 3 \times 2 \times 1$ and $3!$ can be written as $3 \times 2 \times 1.$
Replace $6!$ = $6 \times 5 \times 4 \times 3 \times 2 \times 1$ and $3!$= $3 \times 2 \times 1$ in the following equation,

$${}^6{C_3} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}} \\\ = \dfrac{{6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{3 \times 2 \times 1\left( {3 \times 2 \times 1} \right)}} = \dfrac{{120}}{6} = 20 \\\$$

$\therefore$ The number of triangles that can be formed by joining the vertices of a hexagon is $20$. Hence, option (C) is correct.

Note:
These types of questions always use a combination concept for solving the problem.
Some important definitions you should know
Vertices mean the point where $2$ or more lines meet.
Combination: Any of the ways we can combine things when the order does not matter.
Combination formula: The formula of combination is ${}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}$, where $n$ represents the number of items and $r$ represents the number of the items that being chosen at a time.
The factorial function$(!)$: The factorial function means to multiply all whole numbers from the chosen numbers down to $1$.
The representation of factorial is $n!$.
Alternatively, you can draw the figure and count the triangles but it becomes complicated.