Question
Question: How many roots does the following equation possess $3^{|x|(|2-|x||)} = 1$?...
How many roots does the following equation possess 3∣x∣(∣2−∣x∣∣)=1?
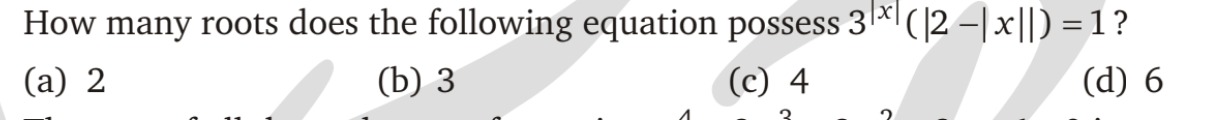
2
3
4
6
3
Solution
The given equation is 3∣x∣(∣2−∣x∣∣)=1.
For any base a>0 and a=1, if ab=1, then the exponent b must be equal to 0. In this case, the base is 3, which is positive and not equal to 1. Therefore, the exponent must be 0:
∣x∣(∣2−∣x∣∣)=0
This equation holds true if either of the factors is zero:
- ∣x∣=0
- ∣2−∣x∣∣=0
Let's solve each case:
Case 1: ∣x∣=0
If the absolute value of x is 0, then x must be 0. So, x=0 is one root.
Case 2: ∣2−∣x∣∣=0
If the absolute value of an expression is 0, then the expression itself must be 0. So, 2−∣x∣=0
Rearranging the term, we get:
∣x∣=2
If the absolute value of x is 2, then x can be 2 or -2. So, x=2 and x=−2 are two more roots.
Combining the roots from both cases, the distinct roots of the equation are x=0, x=2, and x=−2.
Thus, there are 3 roots for the given equation.
