Question

How many rectangles are there in the following figure?

A.$39$
B.$25$
C.$30$
D.$38$

Answer 1

The given question is about to find the number of rectangles in the given figure. In this question, we have to count every small or big rectangle that is made. We will count the total number of rectangles in the following figure by using a combination of identities to count the total number of rectangles.

Complete step-by-step answer:
In the given question, we have to find out the total number of rectangles in the following figure. Here, we will count every small rectangle that is made with a figure.
The given figure is:

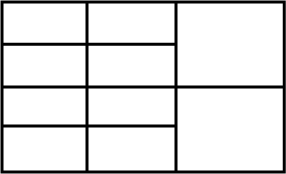
This is the figure from which we have to calculate or count the total number of rectangles that is made here. For calculating the total number of rectangles, firstly we will name the vertices of the rectangle, so that the identification of the rectangle becomes easy.
On naming the vertices of the rectangle, we will make the figure.

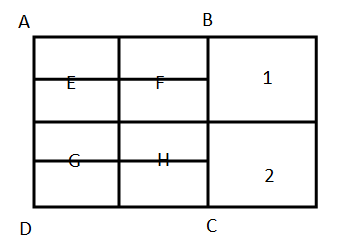
This is the figure of the rectangle after naming the vertices. Here, we have made a partition in upper and lower rectangles too. In order to calculate the total number of rectangles, we will use the formula of combination where combination is nothing but it tells the total number of ways where order matters and the formula for arranging $r$ out of $n$ items, then the total number of way are given by:

n \,}} \right. }}{{\left| \\!{\underline {\, r \,}} \right. \left| \\!{\underline {\, {n - r} \,}} \right. }}$$ Here, total number of rectangles in the figure $$ABCD$$ are: There are $$3$$ vertical lines and $$5$$ horizontal lines, so total number of ways are $${}^5{C_2} \times {}^3{C_2}$$, where $${}^5{C_2}$$ is for horizontal lines taking $$2$$ out of $$5$$ and $${}^3{C_2}$$ is for vertical lines taking $$2$$ out of $$3$$ and on applying the formula of combination, we get: $$\dfrac{{\left| \\!{\underline {\, 5 \,}} \right. }}{{\left| \\!{\underline {\, 2 \,}} \right. \left| \\!{\underline {\, 3 \,}} \right. }} \times \dfrac{{\left| \\!{\underline {\, 3 \,}} \right. }}{{\left| \\!{\underline {\, 2 \,}} \right. \left| \\!{\underline {\, 1 \,}} \right. }}$$ On using the formula of factorial, we get: $$\dfrac{{5 \times 4 \times \left| \\!{\underline {\, 3 \,}} \right. }}{{2 \times 1 \times \left| \\!{\underline {\, 3 \,}} \right. }} \times \dfrac{{3 \times \left| \\!{\underline {\, 2 \,}} \right. }}{{\left| \\!{\underline {\, 2 \,}} \right. \times 1}}$$ $$5 \times 2 \times 3 = 30$$ So, total $$30$$ rectangles. But there are also more rectangles whose naming is: $$1,2,12,1F,1FE,2HG,12FH,12EFGH,2H$$ So, total $$30 + 9 = 39$$ rectangles are there. **So, option (A) is correct.** **Note:** The given question was about to find out the total number of rectangles. We had counted the total number of rectangles made by naming them, by making horizontal and vertical lines. In the same way, we can also find the total number of squares and total number of triangles formed in the other figure.