Question

How many positive numbers $x$ satisfy the equation $\cos \left( {97x} \right) = x$ ?
A) $1$
B) $15$
C) $31$
D) $49$

Answer 1

In the above question, we are given a trigonometric equation $\cos \left( {97x} \right) = x$ . We have to find the number of positive values for which the given equation $\cos \left( {97x} \right) = x$ is satisfied. In order to approach the solution, first we have to check the period of $\cos \left( {97x} \right)$ . As we know that the period of the standard trigonometric function of cosine, i.e. $\cos x$ is $2\pi$ , hence the period of $\cos \left( {97x} \right)$ will be given by $\dfrac{{2\pi }}{{97}}$.

Complete step by step answer:
The trigonometric function is $\cos \left( {97x} \right) = x$ .
We have to find how many positive values of $x$ satisfy the above given equation.
Since the period of cosines function $\cos x$ is $2\pi$ .
Hence, the period of $\cos \left( {97x} \right)$ is $\dfrac{{2\pi }}{{97}}$ .
The range of cosine function, $\cos x$ is $\left[ { - 1,1} \right]$ .
The range of cosine function, $\cos x$ for only positive values is $\left[ {0,1} \right]$ .
Now, since the period of $\cos \left( {97x} \right)$ is $\dfrac{{2\pi }}{{97}}$ ,
Therefore in between the interval $\left[ {0,1} \right]$ , the functions repeats itself, i.e. makes oscillations for about the number of times equal to
$\Rightarrow \dfrac{1}{{\dfrac{{2\pi }}{{97}}}}$
That is,
$\Rightarrow \dfrac{{97}}{2} \times \dfrac{7}{{22}}$
Hence,
$\Rightarrow 15.438$
These are $15$and almost a half times.
Also in each period, the two functions, $\cos \left( {97x} \right)$ and $x$ meet twice.
Therefore,
$\Rightarrow 15.438 \times 2$
That gives,
$\Rightarrow 30.876$
Hence, there is almost one more cycle completed which might have one more value of $x$ .
Therefore, there are total possible positive values of $x$ equal to the number of times,
$\Rightarrow 30 + 1$
That is,
$\Rightarrow 31$
That is the required number of positive values of $x$ .
Therefore, there are $31$ positive numbers $x$ that satisfy the equation $\cos \left( {97x} \right) = x$.

Hence, the correct option is (C).

Note:
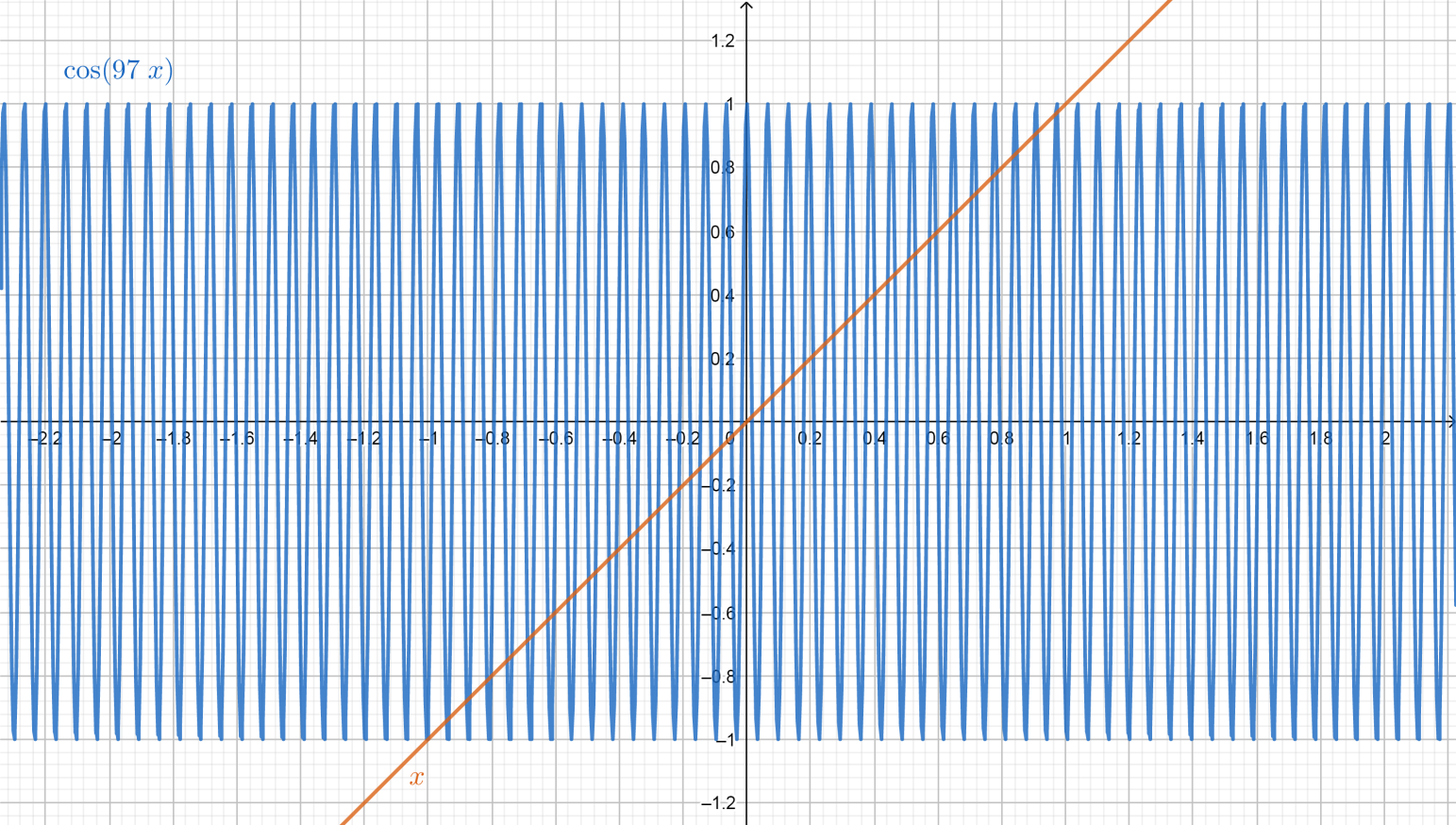
We can also confirm our answer by the graphical method.
Let us suppose two functions $x$ and $\cos \left( {97x} \right)$ .
Now after plotting their graphs we can see that there are $31$intersections in the interval $\left[ {0,1} \right]$ of both the functions.
The graph is given below.