Question

How many planes are present in $4{d_{{z^2}}}$?
a.$2$
b.$1$
c.$Zero$
d.$3$

Answer 1

The planes where there is zero probability region to find the electrons are known as nodal planes. The number of planes is equal to $l$ which is an azimuthal quantum number. We can find the coordinates of these planes by solving the Schrodinger wave equation which is for atoms or molecules to find the shapes of the atomic and molecular orbital.

Complete answer:
Nodal planes are areas that are around the atomic nuclei where the chances of finding electrons are zero. The shape of an atomic orbital is given by the density of the electron cloud, which indicates the chances of finding electrons in the area surrounding the atom or molecule. The denser the cloud would be, the higher we have the chances of finding an electron. Nodal planes lack electron cloud density which implies that the chances of finding electrons in these planes are probably zero. The nodal planes tell us about the wave nature of the electrons because nodes are the point of zero amplitude along with the wave. If there is no amplitude of vibration that means there is no electron density present.
In the question, the structure of $4{d_{{z^2}}}$ is:

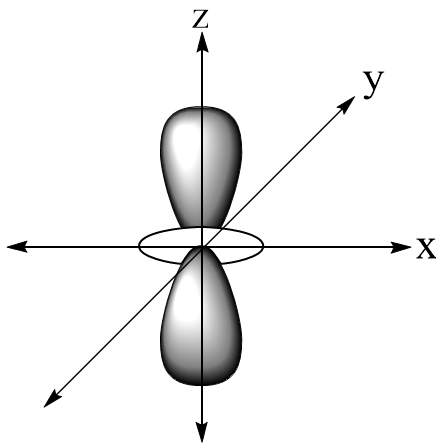
Here we can see that there is the electron density in each plane. A nodal plane is a plane that has zero electron density thus $4{d_{{z^2}}}$ has zero nodal planes.

Thus, option $\left( c \right)$ is correct.

Note:
The point which has zero probability of finding the electron is termed a nodal point. There are two types of nodes:
Radial nodes
Angular nodes