Question

How many four letter passwords can be formed using only the symmetric letters (no repetition allowed).

Answer 1

As we know that in the English alphabets, there are $11$ symmetric alphabets and choosing $4$ out of them is given by ${}^{11}{C_4}$ and then arranging those four alphabets you will get your answer.

Complete step-by-step answer:
Here we have to create the four letter computer password and we need to find the total possibility of a letter that can be made using the symmetric letter.
So here it is saying only the symmetric letter. So what does it mean? So the symmetric letter means that the letter can be divided into equal parts.
For example: we take the alphabet A and we need to find whether the letter is symmetric or not. So we can divide A by the vertical plane

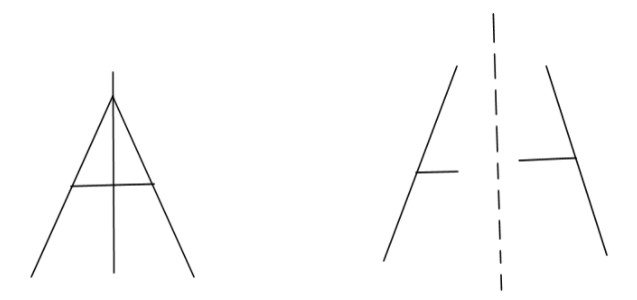
Here both the sides are equivalent hence it is a symmetric alphabet
Similarly, we have total $11$ symmetric alphabets which are A, H, I, O, M, T, U, V, W, X, Z
As we know that in the English alphabets, there are $11$ symmetric alphabets and choosing $4$ out of them is given by ${}^{11}{C_4}$
And we know the formula that
${}^n{C_p} = \dfrac{{n!}}{{(n - p)!p!}}$
So
${}^{11}{C_4} = \dfrac{{11!}}{{(11 - 4)!4!}} = \dfrac{{11!}}{{7!4!}}$
Now if we take the four letters for example: A, H, I, M, then it can be arranged such that no repetition is allowed.
Then the total number of ways to arrange four letters without repetition is $4!$
So here we will get the total number of ways to create a four letter password by using the symmetric letter only will be:
${}^{11}{C_4}(4!) = \dfrac{{11!}}{{7!4!}}(4!)$
$\dfrac{{11 \times 10 \times 9 \times 8 \times 7!}}{{7!}} = 7920$

Note: If we choose four letters out of the eleven and after arranging without repetition is ${}^{11}{P_4}$ ways and if we say that the repetition is allowed then it can be done in ${}^{11}{C_4}\times4^4$ways.