Question

How many different ways are there to arrange the 6 letters in the word SUNDAY?

Answer 1

We use the concepts of permutations to solve this problem. Permutations are related to sorting or arranging of things, in which we have to consider every single case to get a perfect value. We will also learn how to evaluate these permutations.

Complete step by step answer:
Firstly, consider that there are $m$ different things or objects. The number of arrangements of $m$ objects taken $n$ at a time is given by permutations and is represented as ${}^m{P_n}$ and its value is given as ${}^m{P_n} = \dfrac{{m!}}{{\left( {m - n} \right)!}}$
If there are total $m$ objects and all of them have to be arranged in $m$ places, then number of ways of doing so is ${}^m{P_m} = \dfrac{{m!}}{{\left( {m - m} \right)!}} = \dfrac{{m!}}{{0!}} = m!$
In the word SUNDAY, there are 6 letters and no letter is repeating.So, the number of ways of arranging these 6 letters in 6 places is given by ${}^6{P_6} = 6! = 720$. So, there are $720$ ways of arranging the letters of the word SUNDAY.

Let us know step by step.
-Consider that there are 6 places in which we have to arrange the letters of the word SUNDAY.

-Now, we have 6 letters from the word SUNDAY to place in the first position.So, we have 6 ways of arranging a letter in first position, it can be ‘S’ or ’U’ or ‘N’ or ‘D’ or ‘A’ or ‘Y’.
-Now, we have arranged a letter in first position, so there are 5 other letters that have to be arranged in 5 other places.
-So, we have 5 possibilities of arranging a letter from 5 letters in the second position.
-And similarly, there are 4 ways to arrange the remaining 4 letters in third position.
-There are 3 ways to arrange the remaining 3 letters in fourth position.
-There are 2 ways to arrange the remaining 2 letters in fifth position.
-At last, we have only one letter left and one position left and there is only one way to arrange it.

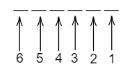
So, the total number of ways of arranging 6 letters of the word SUNDAY will be $6 \times 5 \times 4 \times 3 \times 2 \times 1$ which is equal to $6! = 720$.

Note: We get a positive integer as a result of permutations or combinations. If you get a negative value or a fractional value, then your solution has gone wrong in some way.Selecting a letter can be done by using combinations. Here, we have to select a letter from 6 letters, so it can be done in ${}^6{C_1} = \dfrac{{6!}}{{1!\left( {6 - 1} \right)!}} = \dfrac{{6!}}{{5!}} = 6$. So, selecting letters can be done in this way.