Question

How many atoms of $PC{{l}_{5}}$lie in the same plane?

Answer 1

To answer this question we must know about the geometry and shape of $PC{{l}_{5}}$molecule. The hybridization of $PC{{l}_{5}}$molecule is$s{{p}^{3}}d$. The geometry of $PC{{l}_{5}}$molecule is triangular bipyramidal.

Complete step by step solution:
Let’s try to understand $s{{p}^{3}}d$hybridization.
In $PC{{l}_{5}}$molecule, $s{{p}^{3}}d$hybridization is present. This means that 5 orbitals are present in this molecule that take part in hybridization. These orbitals pool their energy and form 5 hybrid orbitals of similar energy and other similar properties.

The orbitals involved in this hybridization are:
$s+{{p}_{x}}+{{p}_{y}}+{{p}_{z}}+{{d}_{{{z}^{2}}}}$
This geometry is then further divided into two parts
1. $s+{{p}_{x}}+{{p}_{y}}$, the mixing of these three orbitals give a planar geometry. This geometry is known as triangular planar.
2. ${{p}_{z}}+{{d}_{{{z}^{2}}}}$, the mixing of these two orbitals gives a linear geometry. This geometry is known as linear only.
Therefore, three atoms $PC{{l}_{5}}$ molecules are present in a plane. These three atoms of Cl along with P make triangular planar geometry. While the remaining two atoms of Cl are in a linear geometry with P atoms.

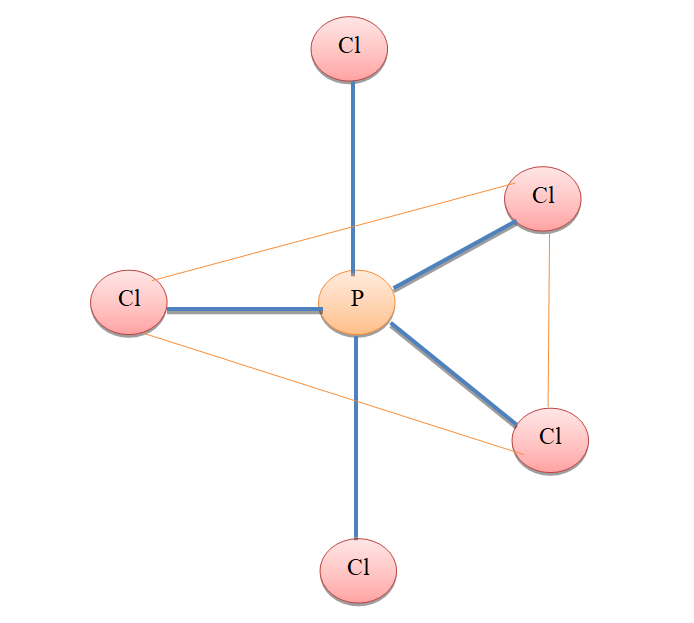
In the molecule, $PC{{l}_{5}}$ there is a definite geometry. This is because of the stability of the molecule. In triangular bipyramidal geometry, the repulsive forces are minimal. So, the $PC{{l}_{5}}$molecule is stable and hence adopts a particular geometry.

Hence, the number of atoms in the same plane in $PC{{l}_{5}}$molecule is 4.

Note: Molecules having $s{{p}^{3}}d$ hybridization can have two different geometries based on the types of central atoms. The two geometries are triangular bipyramidal and square pyramidal. The difference in the geometries is due to the central atom. If the central atom is a transition metal then it does not take triangular bipyramidal geometry.