Question

How many acute and obtuse angles does a rhombus have?

Answer 1

Use the properties of rhombus, like any rhombus have four interior angles which sums up to ${360^0}$ , also rhombus have two sets of equivalent opposite interior angles and last but not least rhombus have two sets of adjacent supplementary angles. Use these above properties and also draw a rhombus to find the numbers of acute and obtuse angles.

Complete step by step solution:
To find the numbers of acute and obtuse angles in rhombus, let us go through its properties first. A rhombus has two sets of equal opposite interior angles, and also it has a total of four interior angles which sums up to ${360^0}$ and two sets of adjacent supplementary angles, that is their sum is equal to ${180^0}$. Let us draw a rhombus to understand its properties more.

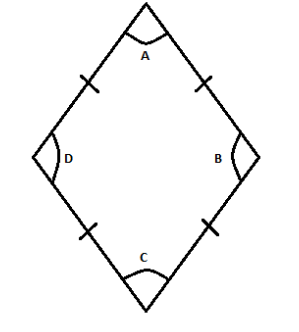
In these figure according to properties of rhombus,
$
\angle {\text{A}} = \angle {\text{C}};{\text{and}};\angle {\text{B}} = \angle {\text{D}} \\
{\text{Also,}};\angle {\text{A + }}\angle {\text{C + }}\angle {\text{B + }}\angle {\text{D}},{\text{ =
36}}{{\text{0}}^0} \\
{\text{And}};\angle {\text{A}};{\text{ + }}\angle {\text{C}}; = \angle {\text{B}};{\text{ + }}\angle
{\text{D}};{\text{ = 18}}{{\text{0}}^0} \\

$

Since there is no right angle in the figure and from the third equation $\angle {\text{A}}\;{\text{ + }}\angle {\text{C}}\; = \angle {\text{B}}\;{\text{ + }}\angle {\text{D}}\;{\text{ = 18}}{{\text{0}}^0}$

We can say that one angle in the pair of adjacent angles, one is acute and another is obtuse because if both are obtuse or acute angles then their sum will be greater than ${180^0}$ or less than ${180^0}$.

$\because$ there are two pairs of adjacent angles,

$\therefore$ there are two acute angles (one in each pair) and two obtuse angles (one in each pair) present in a rhombus.

Note: A rhombus is a four sided polygon which looks like a diamond shape having all of its four sides equal in length. If we talk about its interior angles, then rhombus is also a type of parallelogram that is, it has its opposite sides parallel to each other.