Question

How many $176\Omega$resistors (in parallel) are required to carry $5A$ in $220V$ line?

Answer 1

The equation for the net resistance for two resistors of resistances connected in parallel hast to be used first.
Further, Ohm's law and Kirchoff’s current law will also be used to find the number of resistors.

Formula used:
The net resistance for two resistors of three resistances $({R_1}),({R_2})$and $\left( {{R_3}} \right)$ connected in parallel will be in relation
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
Ohm's law 🡪$V = IR = > I = \dfrac{V}{R}$
Kirchoff's current law 🡪$I = {I_1} + {I_2} + {I_3}$

Complete step-by-step solution:
Let's find out how a parallel resistance circuit works. A parallel resistance circuit is
made below.

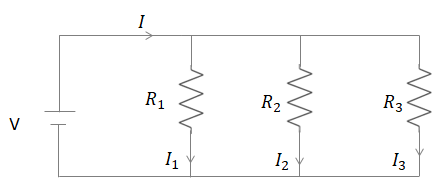
The voltage source is $(V)$ and the net amount of current flowing through the circuit is $(I)$. There are three resistances $({R_1}),({R_2})$ and $\left( {{R_3}} \right)$which are connected in parallel to each other. The amount of current passed through each branch of the resistor is given by: $\left( {{I_1}} \right),\left( {{I_2}} \right)$and $\left( {{I_3}} \right).$
The values of the individual amount of current through each resistance can be found through Ohm's law$V = IR = > I = \dfrac{V}{R}$
Hence, the value $({I_1})$is ${I_2} = \dfrac{V}{{{R_2}}}$and the value $({I_3})$is${I_3} = \dfrac{V}{{{R_3}}}$
Using Kirchoff's current law$I = {I_1} + {I_2} + {I_3}$
Hence,$I = {I_1} + {I_2} + {I_3}$ becomes
$I = {I_1} + {I_2} + {I_3}$
$\Rightarrow \dfrac{V}{R} = \dfrac{V}{{{R_1}}} + \dfrac{V}{{{R_2}}} + \dfrac{V}{{{R_3}}}$
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
Let's consider a special case of the resistances connected in parallel. In this case, the resistances are of the same value, that is $\dfrac{1}{{{R^/}}} = \dfrac{1}{R} + \dfrac{1}{R} + \dfrac{1}{R} = = > \dfrac{1}{{{R^/}}} = \dfrac{3}{R} = = > {R^/} = \dfrac{R}{3}$
Hence, the net resistance of the circuit becomes one-third the value of the resistance in each of the branches. Using the same formulation for $N$ branches, we get
${R_{net}} = \dfrac{R}{N}$-----🡪(1)
Where$(R)$is the resistance of each branch and $(N)$is the number of branches
For the current problem, we have multiple $176\Omega$ in parallel to each other. These
are connected to $220V$the line and the net current is $5A$ Hence using Ohm's law
and the value of resistance from the equation $(1)$, we get
$V = I{R_{net}} = = > 220 = 5(\dfrac{{176}}{N}) = = > N = (\dfrac{{176}}{{44}}) = = > N = 4$
Hence, 4 of the $176\Omega$resistors in parallel would be required to get a net current
of $5A$ flowing through a $220V$ line.

Note: It's important to remember that in a parallel resistance circuit connection, the voltage drawn by all the resistances is equal. An everyday example of this is the way electricity reaches all our houses. The constant $220V$ voltage is supplied to all the households in a locality since all the houses are in a parallel connection to each other.