Question

How is trigonometric substitution different from u substitution?

Answer 1

In mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions. It is a technique for evaluating integrals with the help of calculus concepts. A trigonometric substitution is used for integrals of the form ${x^2} \pm {a^2}$ or $\sqrt {{x^2} \pm {a^2}}$. U-substitution is used when a function and its derivative appears in the integral.

Complete step-by-step answer:
Let us first consider the trigonometric substitution.
Here, we will use the two most important concepts of trigonometry that are the Pythagoras theorem and its identities.
Pythagoras theorem relates two sides of the right-angle triangle to the hypotenuse.
Let us understand with the help of a figure.

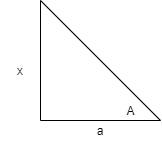
In the above figure, two sides are x and a, and hypotenuse will be as follow:
According to Pythagoras theorem,
$hypotenus{e^2} = bas{e^2} + perpendicula{r^2}$
$\Rightarrow hypotenus{e^2} = {a^2} + {x^2}$
From the above figure, we can also write the trigonometric ratios of angle A.
For example,
$\Rightarrow \tan A = \dfrac{x}{a}$
We can also write as,
$\Rightarrow a\tan A = x$
Put the value of x in ${a^2} + {x^2}$.
${a^2} + {a^2}{\tan ^2}A$
So,
$\Rightarrow {a^2}\left( {1 + {{\tan }^2}A} \right)$
That is equal to,
$\Rightarrow {a^2}{\sec ^2}A$
Then find the integral.
Now, let us consider u-substitution.
We use this technique when we have something like $\int {\dfrac{{\ln x}}{x}dx}$.
Here, we can see two functions: $\ln x$ and $\dfrac{1}{x}$ .
And we know the derivative concepts, $\dfrac{{d(\ln x)}}{{dx}} = \dfrac{1}{x}$ for all x>0.
So, we will take the value of u as $\ln x$.
Then $\dfrac{{du}}{{dx}} = \dfrac{1}{x}$ and
So that, $du = \dfrac{1}{x}dx$.
Then find the integral.
Using u-substitution, the calculation is easier than trigonometric substitution.

Note:
While these two techniques may differ, they both serve the same purpose. And the purpose is to reduce an integral to a simpler form. So, we can use the basic techniques of integral. A trigonometric substitution is used for integrals of the form ${x^2} \pm {a^2}$ or $\sqrt {{x^2} \pm {a^2}}$.