Question

How is the refractive index of a material related to real and apparent depth ?

Answer 1

Consider a material and a ray of light falling on its surface at some angle $\theta$. The ray of light will refract. Relate the angles made by line of sight and the refracted ray and represent it in terms of refractive index $\mu$.

Complete step by step answer: First we will understand in brief the meaning of real and apparent depth and then proceed to our derivation of relation between them in terms of refractive index.
An object placed in a denser medium when viewed from a rarer medium appears to be at a depth less than the real depth. This depth is the apparent depth and this happens due to refraction of light.

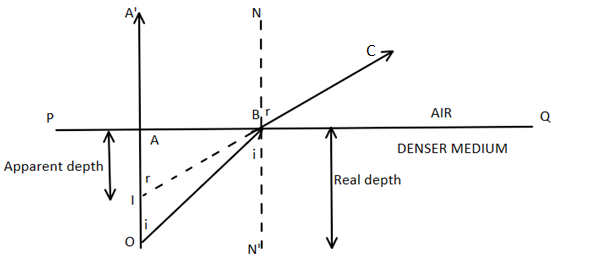
Now we will proceed towards our derivation.
Consider a point object $O$ kept at the bottom of a transparent medium. Let $PQ$ be the surface that separates the medium and air.
Now we will consider two rays emerging out from our point object $O$.
First of all we will consider ray $OA$ which is incident on surface $PQ$ normally such that it passes undeviated. The second ray that we will consider is ray $OB$ which strikes the boundary surface $PQ$ at $B$and suffers refraction.
We should keep in mind the fact that when a ray travels from denser to rarer medium, it bends away from the normal and so does our ray $OB$.
When viewed by the eye, the ray $BC$ appears to be coming from point $I$. This point actually represents the virtual image of the object $O$. So our object $O$ will always appear to us at less depth that is $AI$ in this case and not the actual depth $AO$. Now we will represent the whole phenomenon mathematically.
For incident ray $OB$, the angle of incidence $i = \angle OBN'$ and $r = \angle CBN$
Since, $AO$ and $BN'$ are parallel, and $OB$ is the transversal line, we can say that
$\angle AOB = \angle OBN' = i$
Similarly,
$IA'$and $BN$ are parallel and $IC$ is the transversal line, so
$\angle BIA' = \angle CBN = r$
Now we will use some basic trigonometric relations.
In right angled $\triangle BAO$,
$\sin i = \dfrac{{BA}}{{OB}}$
In right angled $\triangle IAB$
$\sin r = \dfrac{{BA}}{{IB}}$
We need to now recall the Snell’s law which says that the refractive index of air with respect to a medium $_m{\mu _a} = \dfrac{{\sin i}}{{\sin r}}$
Substituting the above values
$\mu = \dfrac{{\dfrac{{BA}}{{OB}}}}{{\dfrac{{BA}}{{IB}}}} = \dfrac{{IB}}{{OB}}$
Refractive index of medium with respect to air
$_a{\mu _m} = \dfrac{1}{{_m{\mu _a}}} = \dfrac{{OB}}{{IB}}$

Since the point $B$ is very close to point $A$ in reality, we can approximate $IB = IA,OB = OA$
Hence, $_a{\mu _m} = \dfrac{{OA}}{{IA}} =$Real depth$\div$Apparent depth.

Note: You should have a firm grip on basic concepts of trigonometry and should be familiar with the phenomenon of refraction, reflection, etc. and should be well versed with the laws associated with them.