Solveeit Logo
Login

Question

Question: How is the graph of \[f(x) = x{}^2 - \,4\] related to that of \[f(x) = x{}^2\] ?...

How is the graph of f(x)=x2− 4f(x) = x{}^2 - \,4 related to that of f(x)=x2f(x) = x{}^2 ?

Explanation

Solution

Hint : The above question is related to the transformation of graphs. The original graph of the equation f(x)=x2f(x) = x{}^2 is an upward opening parabola with vertex at origin. In the new equation f(x)=x2− 4f(x) = x{}^2 - \,4 ,the function change is along the y-axis. The remaining nature of the parabola remains the same. Thus it is only required to shift the vertex of the original equation to obtain the new one.

Complete step-by-step answer :
The function f(x)=x2− 4f(x) = x{}^2 - \,4 can be written as x2=f(x)+4{x^2} = f(x) + 4 and the function f(x)=x2f(x) = x{}^2 can be written as x2=f(x){x^2} = f(x) . Now the function x2=f(x){x^2} = f(x) represents an upward opening parabola with its vertex at origin. Now, if we compare the second equation x2=f(x)+4{x^2} = f(x) + 4 with the first one, we can see that that the left hand side of both the equations are same but the right hand side of second equation is 4 units less than the previous one.
Therefore, the equation f(x)=x2− 4f(x) = x{}^2 - \,4 can be obtained by shifting the equation f(x)=x2f(x) = x{}^2 four units in the downward direction. Hence the graph is transformed as below.

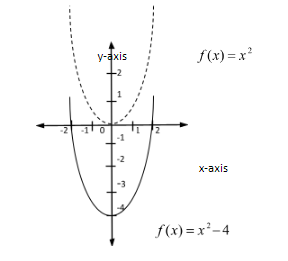
Hence we can observe that the graph of the equation f(x)=x2− 4f(x) = x{}^2 - \,4 can be obtained by shifting the graph of the equation f(x)=x2f(x) = x{}^2 along the y-axis in the negative direction.

Note : There are some basic graphical transformations of parabolas which are to be noted. The function f(x)=x2+bf(x) = x{}^2 + b has a graph which simply looks like the standard parabola f(x)=x2f(x) = x{}^2 with its vertex shifted b  unitsb\,\,units along the y-axis. Thus the vertex will be located at (0,b)(0,b) . if bb is a positive value then the parabola moves b unitsb\,units upwards and if the value of bb is negative then the parabola moves b  unitsb\,\,units downward. Another form of parabola has the equation f(x)=(x−a)2f(x) = {(x - a)^2} which has the graph same of that of f(x)=x2f(x) = x{}^2 with its vertex shifted a  unitsa\,\,units along x-axis. If aa is positive it shifts a  unitsa\,\,units to the right and if the value of aa is negative it shifts a  unitsa\,\,units to the left .The the vertex of the parabola changes to (a,0)(a,0) .
These two types of transformation can be combined to produce a parabola which is congruent to the basic parabola but with vertex at (a,b)(a,b) .