Question

How is sin calculated?

Answer 1

In a right triangle, sin of an angle is the length of the side opposite to it divided by the length of the hypotenuse of the angle. i.e.
$\sin (angle)=\dfrac{length \;of \;opposite \;side}{length \;of\; hypotenuse}$

Complete step by step solution:
Consider a right angled triangle ABC such that

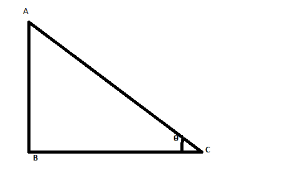
The sine of angle $\theta$ is given as
$\sin \theta =\dfrac{AB}{AC}$
Here, as we can see in the figure , the side AB is called the perpendicular of the triangle and the side BC as the base whereas the side AC is called the hypotenuse of the triangle.
Therefore, we can write that

& AB=P \\\ & BC=B \\\ & AC=H \\\ \end{aligned}$$ Such that $$\sin \theta =\dfrac{P}{H}$$ Formula used: An angle which forms the part of a right angled triangle, it is very easy to determine the sine function of that angle. The formula used to determine sine of an angle is $$\sin \theta =\dfrac{P}{H}$$ Where, $$P$$ is the perpendicular of the triangle and $$H$$ is the hypotenuse of the triangle. Additional information: The other trigonometric functions of the angle can be defined similarly; for example, the cosine of the angle is the ratio between the adjacent side and the hypotenuse, while the tangent gives the ratio between the opposite and adjacent sides **So, the correct answer is “ $$\sin \theta =\dfrac{P}{H}$$ ”.** **Note** : It is very important to carefully recognize the three sides of the triangle. Confusing base with perpendicular can convert sine to cosine or vice versa. Similarly, taking the longest side only as the hypotenuse is very important. The value of $$\sin \theta $$ lies in the range between the values $$\left[ -1,+1 \right] $$ so if you get any value that is less than $$-1$$ or more than $$+1$$ denotes a calculation mistake.