Question

How high a column of air would be necessary to cause the barometer to read 76cm Hg . If the atmosphere were in uniform density $1.2$ $kg/{m^3}$. The density of the mercury is $13.6 \times {10^3}$ $kg/{m^3}$

Answer 1

The density is equal to mass per volume A barometer is a device which measures atmospheric pressure. Whenever there is a change in the atmosphere the height will change . Here the density of Mercury is given $13.6 \times {10^3}$ $kg/{m^3}$. Also we are having uniform density of atmosphere that is $1.2$ $kg/{m^3}$. We need to find the density of mercury and atmosphere and divide the equations to get the correct answer.

Complete step by step answer:
$\Rightarrow$ density of mercury = $\dfrac{{mass}}{{volume}}$
As the question have given us the column of mercury is $76$ $cm$
$\Rightarrow$ density of mercury $\left( {{d_1}} \right)$ = $\dfrac{{mass}}{{area \times 76}}$ ………………...$\left( 1 \right)$

let us take the column if air be $x$
$\Rightarrow$ density of atmosphere =$\dfrac{{mass}}{{volume}}$
$\Rightarrow$ density of atmosphere $\left( {{d_2}} \right)$ =$\dfrac{{mass}}{{area \times x}}$ ……………………….$\left( 2 \right)$
now divide the equation $1$ and equation $2$
$\Rightarrow$ $\dfrac{{{d_1}}}{{{d_2}}}$=$\dfrac{{mass}}{{area \times 76}}$ $\times \dfrac{{area \times x}}{{mass}}$
$\Rightarrow$ $\dfrac{{{d_1}}}{{{d_2}}}$= $\dfrac{x}{{76}}$
$\Rightarrow$ $\dfrac{{13.6 \times {{10}^3}}}{{1.2}}$=$\dfrac{x}{{76}}$
$\Rightarrow$ $\dfrac{{13.6 \times {{10}^3}}}{{1.2}} \times 76$ =$x$
$\Rightarrow$ $8613$=$x$
So the answer is $$8613$$$cm$.

Hence, the correct option is C.

Additional Information: Mercury Barometer in which atmospheric pressure is balanced by the column of mercury and the height is measured . It was invented by Evangelista Torricelli.

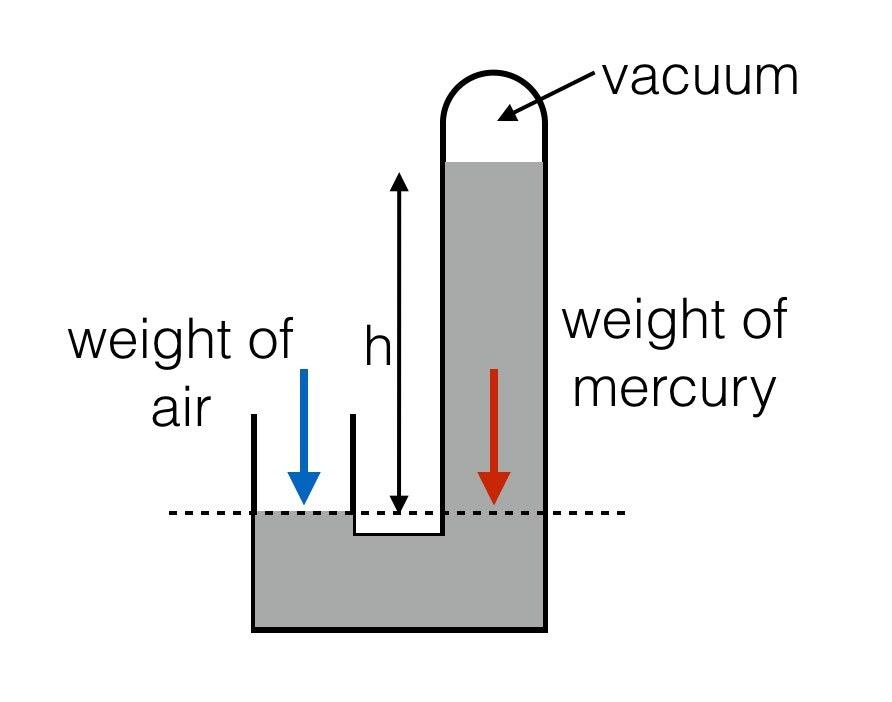
This is the oldest form of barometer where mercury is used. In this device by measuring the height of the column we can calculate the atmospheric pressure. The dotted line which is formed is the point below which the air pressure which is trying to down the level in the left must be the same pressure excreted by the mercury to down the level in the right.

Note: Density is measured by mass per volume , and volume is $l \times b \times h$ . Find density , first for mercury and after it find density for atmosphere and divide both equations . when we will divide the mass and area will get cancelled and we can easily find our answer by cross multiplication.