Question

How does the period of an oscillation in a spring-mass system depend on mass and amplitude? How can I express this graphically for period as a function of mass, period as a function of the square root of the mass, and period as a function of amplitude?

Answer 1

In order to answer the following question, we will be describing the most basic spring-mass system. We will derive the equation of the time period of oscillations of such a system. Finally, we will represent the graph of time period with different types of variables as asked in the question.

Formula used:
Time period of oscillation: $T=2\pi \sqrt{\dfrac{m}{k}}$
Where $m$ is the mass and $k$ is the spring constant.

Complete step by step answer:
First of all, we will draw a simple diagram of a spring-mass system.

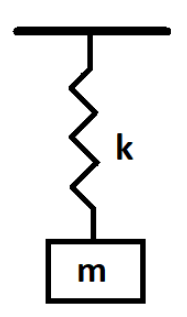
As we can see from the figure, a mass$(m)$ is suspended with the help of a spring having a spring constant of ($k$). If the spring is stretched and then released, the spring-mass system will oscillate. The formulae for time period for such oscillation is given by
$T=2\pi \sqrt{\dfrac{m}{k}}$
If we square both sides of the above equation, the equation becomes
$\therefore {{T}^{2}}=4{{\pi }^{2}}\dfrac{m}{k}$
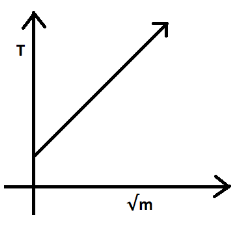
The above equation implies that the time period of oscillation is directly proportional to the square root of mass. It also states that the time period is independent of the amplitude.Therefore, if we plot a graph of $T$ vs $m$ , we will have a square root graph

Now, if we plot a graph of $T$ vs $\sqrt{m}$, then we get a linear graph with a gradient equal to $\dfrac{2\pi }{\sqrt{k}}$

Lastly, the graph of $T$ vs $A$ (amplitude) will represent a horizontal line as time period is independent of amplitude.

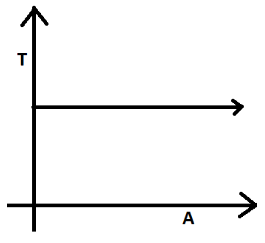
Note: It is very important to keep in mind that the graph of $T$ vs $A$ will give you a horizontal line because time period is independent of amplitude and will remain constant with change in amplitude. Now, if the spring is overstretched or if it jumps, then this dependence may vary and the graph will not be a horizontal line.