Question
Question: How does soh cah toa apply to a right angle triangle ?...
How does soh cah toa apply to a right angle triangle ?
Solution
In order to find a solution to this problem, we have to be able to recognize what type of question it is. As we can see, this is a problem of trigonometric function. It states the formula that is used in trigonometric function and that is applied to a right angle triangle.
Complete step by step solution:
In geometry, trigonometric functions are the functions that are used to find the unknown angle or side of a right-angled triangle.
There are three basic trigonometric functions: Sine, Cosine and Tangent.
The angles of sine, cosine, and tangent are the primary classification of functions of trigonometry. And the three functions which are cotangent, secant and cosecant can be derived from the primary functions. So Basically, the other three functions are often used as compared to the primary trigonometric functions.
If θ is an angle of a right-angled triangle, then the trigonometry functions are given by:
Now consider the right angle triangle ABC. Let angle A be angle θ
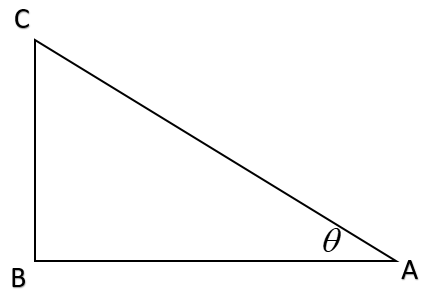
sinθ = Opposite Side of angle θ/Hypotenuse
⇒sinθ=ACBC
cosθ = Adjacent Side of angle θ/Hypotenuse
⇒cosθ=ACAB
tanθ = Opposite Side of angle θ/Adjacent
⇒tanθ=ABBC
cotθ = Adjacent Side of angle θ/Opposite
⇒BCAB
secθ = Hypotenuse/Adjacent Side of angle θ
⇒secθ=ABAC
cosecθ = Hypotenuse/Opposite Side of angle θ
⇒cscθ=BCAC
That is can be denoted as:
sinθ=hypotenuseoppositecosθ=hypotenuseadjacenttanθ=adjacentoppositecotθ=tanθ1=oppositeadjacentsecθ=cosθ1=adjacenthypotenusecosecθ=sinθ1=oppositehypotenuse
We can remember this trigonometric functions by making use of mnemonics that is,
soa, cah, toa
This means,
soh:
Sin = Opposite over Hypotenuse
cah:
Cos = Adjacent over Hypotenuse
toa:
Tan = Opposite over Adjacent
Therefore, these are a set of mnemonics to help remember how to derive the basic trigonometric functions for a (non-right) angle of a right triangle.
Note:
Trigonometric functions are also known as a Circular Functions can be simply defined as the functions of an angle of a triangle. It means that the relationship between the angles and sides of a triangle are given by these trig functions. The basic trigonometric functions are sine, cosine, tangent, cotangent, secant and cosecant.
Also, the above mnemonics can only apply to right angle triangles.
