Question

How does slope intercept differ from the standard form?

Answer 1

Assuming here the question talks about the various forms of lines, slope intercept form of the line gives us a direct representation of the slope as well as the intercept it cuts on the y axis whereas the standard form doesn’t give us a direct representation.

Complete step by step answer:
The equation of the standard form of the line is $ax+by+c=0$.Where $a$ is the coefficient of $x$, $b$ is the coefficient of $y$ and $c$ is a constant.
This equation is just a standard form of the line which doesn’t really tell us much about anything except for all the points that satisfy this equation upon plugging them in. And also, upon differentiation, it can tell us about the slope of the line.
If the value of the constant $c$ is 0, then line passes through origin (0,0). The graph of a line taken in the standard form or the intercept form remains the same as both these forms are representing the same line.
Let’s take an example of line, say, $2x+y=4$. We can talk about all the points that satisfy this equation.

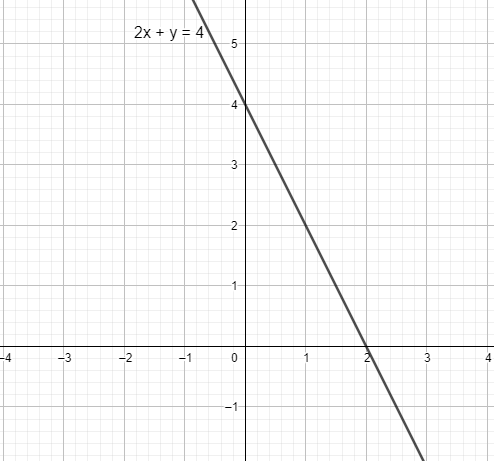
As we can see from the graph, all the above points satisfy the equation.
Now if we talk about slope intercept form the line, the equation is $y=mx+c$ where $m$ is the slope of the line and $c$ here a constant and also specifies the length of the intercept the line cuts on the $y$ axis when the value of $x$ is 0.
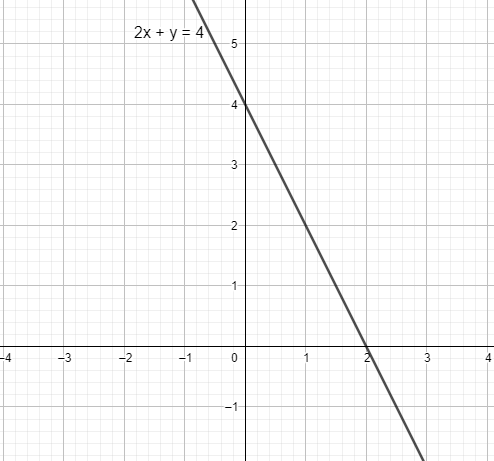
Let’s take the same example that we have previously used. The equation of the line is $2x+y=4$. Now, let’s convert this into slope intercept form. Taking the $x$ term onto the right-hand side of the equation we get the following:
$\Rightarrow$ $y=4-2x$, where 4 is the length of the intercept and -2 is the slope of the line.
As I have stated earlier, the graph of the two equations remains the same.

Note:
Please carefully compare the coefficient of the given line to the standard equation, in order to get the intercept and slope correct. Also, having these standard equations at your finger -tips can make you quickly solve these questions.