Question

How does $\sin x=0$ equals $\pi$?

Answer 1

In this problem, we have to find how $\sin x=0$ equals $\pi$. We should always know that the sine value is always equal to zero for every multiple of $\pi$, where $\pi$ radians is equal to ${{180}^{\circ }}$. We can now draw a graph with a sine curve to see the value of sine for $\pi$.

Complete step by step answer:
We know that the given trigonometric function given is sine.
We should always remember that the sine value is always equal to zero for every multiple of $\pi$, where $\pi$ radians is equal to ${{180}^{\circ }}$.
We can now draw a graph with a sine curve to see the value of sine for $\pi$.

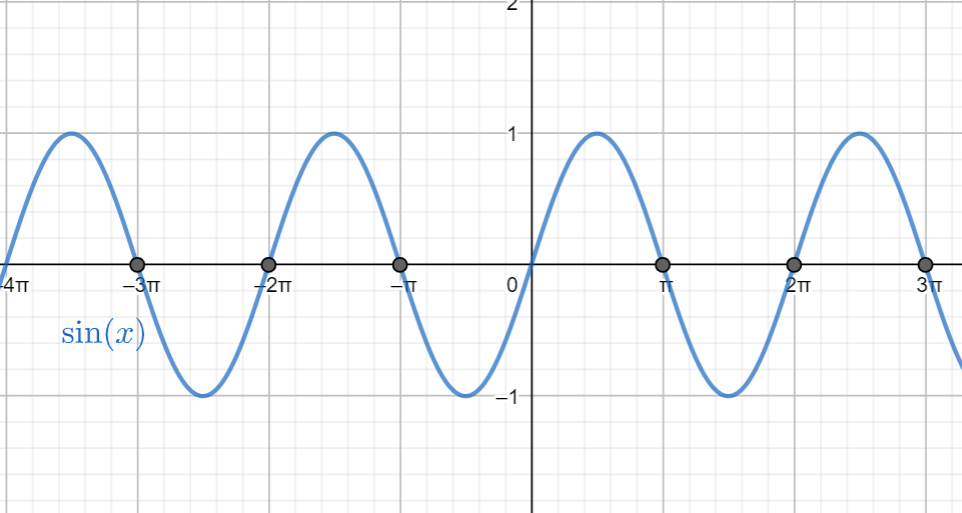
We can now see that the sine curve touches the line at 0 in every multiple of $\pi$.
We can now write it as,
$\Rightarrow \sin x=0\to x=k\times \pi$
Where k is any whole number.
Therefore, we can summarize that every multiple of $\pi$ for the sine function is always equal to zero.

Note: Students should also remember that $\pi$ radians is equal to ${{180}^{\circ }}$. We should also know that the sine function goes from 0 to ${{90}^{\circ }}=\dfrac{\pi }{2}$and then back to 0 to ${{180}^{\circ }}=\pi$, and when we come down to -1 to ${{270}^{\circ }}=\dfrac{3\pi }{2}$ and when we go up to 0 again at ${{360}^{\circ }}=2\pi$, therefore, it will be 0 at every multiple of $\pi$. We should also concentrate in the graph part while drawing the sine curve.