Question

How does one find the exact value for $\sin (\dfrac{\pi }{4})$ ?

Answer 1

For solving this particular question you have to consider an isosceles right-angled triangle then you have to use Pythagoras Theorem which says $A{C^2} = A{B^2} + B{C^2}$ , after using this Theorem we get the relationship between hypotenuse and length of the other two side. Lastly use a trigonometric formula which says $\sin \theta = \dfrac{p}{h}$ , where $p$ represent length of perpendicular side and $h$ represent length of hypotenuse side.

Complete step by step solution:
For solving the particular question that is $\sin (\dfrac{\pi }{4})$ ,
We have to consider an isosceles right-angled triangle ,
Let us consider a $\Delta ABC$ which is isosceles and right angle at $B$ ,

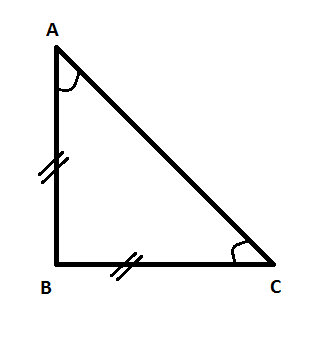
Here
$\angle A = \angle C = {45^ \circ } \\\ and \\\ \angle B = {90^ \circ } \\\$
And being an isosceles triangle side $AB$ is equal to side $BC$ ,
Suppose
$AB = BC = a \\\ and \\\ AC = h \\\$
Now using Pythagoras Theorem which says $A{C^2} = A{B^2} + B{C^2}$ ,
We can write,
$\Rightarrow {h^2} = {a^2} + {a^2} \\\ \Rightarrow {h^2} = 2{a^2} \\\ \Rightarrow h = \sqrt 2 a \\\$
And from trigonometry we also know that $\sin \theta = \dfrac{p}{h}$ , where $p$ represent length of perpendicular side and $h$ represent length of hypotenuse side.
$\Rightarrow \sin C = \dfrac{{AB}}{{AC}} \\\ \Rightarrow \sin (\dfrac{\pi }{4}) = \dfrac{a}{h} \\\$
And earlier we see that $h = \sqrt 2 a$ ,
Now put this value , we get,
$\Rightarrow \sin (\dfrac{\pi }{4}) = \dfrac{a}{{\sqrt 2 a}} \\\ \Rightarrow \sin (\dfrac{\pi }{4}) = \dfrac{1}{{\sqrt 2 }} \\\$
And here we get the required result.

Note: You must know that sin, cosine, and tangent are considered as major trigonometric functions, hence we can derive the solutions for the equations comprising these trigonometric functions or ratios. We can also derive the solutions for the other three trigonometric functions such as secant, cosecant, and cotangent with the help of the solutions which are already derived.