Question

How do you write the vertex form equation of the Parabola $x = {y^2} + 6y + 1$?

Answer 1

Here, we will use the completing the square method to simplify the equation. Then by using the suitable algebraic identity we will convert the equation into vertex form of the Parabola. A parabola is a U- shaped curve which is at an equal distance from the fixed point and the fixed straight line.

Formula Used:
We will use the following formulas:
1. Completing the square method is given by the formula $a{y^2} + by + c = {\left( {y \pm \dfrac{b}{2}} \right)^2} + c + {\left( {\dfrac{b}{2}} \right)^2}$
2. The square of the sum of the numbers is given by the algebraic identity ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$
3. Equation of Parabola in the Vertex form is given by $x = a{\left( {y - k} \right)^2} + h$ where $\left( {h,k} \right)$ be the coordinates of the vertex of a Parabola and $a$ is the multiplier.

Complete step by step solution:
We are given an equation of Parabola $x = {y^2} + 6y + 1$.
Now, we will use the completing square method to convert the quadratic equation into the vertex form.
Now, we will group the $y$- term on one side of the equation and the $x$- term and the constant term on the other side of the equation, we get
Completing the square method is given by the formula $a{y^2} + by + c = {\left( {y \pm \dfrac{b}{2}} \right)^2} + c + {\left( {\dfrac{b}{2}} \right)^2}$
Quadratic equation $\left( {{y^2} + 6y} \right)$ is of the form $a{y^2} + by + c = 0$.
Comparing the given quadratic equation, we get $a = 1$ and $b = 6$.
Now, by using the completing the square method for the $y$- term, we get
$x - 1 + {\left( {\dfrac{6}{2}} \right)^2} = {y^2} + \dfrac{6}{2}y + {\left( {\dfrac{6}{2}} \right)^2}$
By simplifying the equation, we get
$\Rightarrow x - 1 + {\left( 3 \right)^2} = {y^2} + 3y + {\left( 3 \right)^2}$
Applying the exponent on the terms, we get
$\Rightarrow x - 1 + 9 = {y^2} + 3y + 9$
Subtracting the like terms on RHS, we get
$\Rightarrow x + 8 = {y^2} + 3y + 9$
The square of the sum of the numbers is given by the algebraic identity ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$ .
Now, by using the algebraic identity, we get
$\Rightarrow x + 8 = {\left( {y + 3} \right)^2}$
Subtracting 8 from both sides, we get
$\Rightarrow x = {\left( {y + 3} \right)^2} - 8$
We know that the equation of Parabola in the Vertex form is given by $x = a{\left( {y - k} \right)^2} + h$ where $\left( {h,k} \right)$ be the coordinates of the vertex of a Parabola and $a$ is the multiplier.
Now, we will write the vertex form for the given equation by using the general vertex form of the Parabola. Therefore, we get
$x = {\left( {y + 3} \right)^2} - 8$
So, the vertex of the Parabola $\left( {h,k} \right)$ is$\left( { - 8, - 3} \right)$ and the multiplier $a$ is $1$.
Now, we will draw the Parabola with the vertex $\left( { - 8, - 3} \right)$.

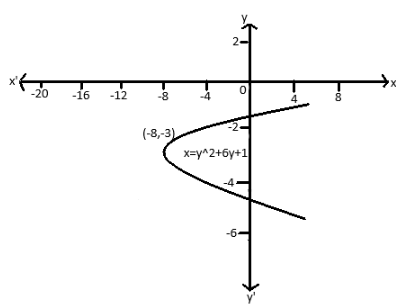
Therefore, the vertex form of the given equation of Parabola $x = {y^2} + 6y + 1$ is $x = {\left( {y + 3} \right)^2} - 8$.

Note:
We know that a parabola is symmetric with its axis. If the equation has ${y^2}$ term, then the axis of symmetry is along the x-axis and if the equation has ${x^2}$ term, then the axis of symmetry is along the y-axis. We should know that the vertex of a Parabola is the minimum or maximum point of a Parabola. We will find the type of Parabola, by using the sign of the multiplier $a$ in the vertex form of the parabola. If $a$ is positive in $x = a{(y - k)^2} + h$, then the parabola is open rightwards and if $a$ is negative in $x = a{(y - k)^2} + h$, then the parabola is open leftwards. So, the given equation of Parabola is open rightwards.