Question

How do you write the vertex form equation of the Parabola $y = {x^2} + 6$ ?

Answer 1

Here, we will use the general vertex form of the Parabola to rewrite the given equation of Parabola in the form of vertex form of a Parabola. A parabola is a U- shaped curve which is at an equal distance from the fixed point and the fixed straight line.

Complete step by step solution:
We are given an equation of Parabola $y = {x^2} + 6$.
Now, we will write the vertex form for the equation of Parabola.
We know that the equation of Parabola in the Vertex form is given by $y = a{\left( {x - h} \right)^2} + k$ where $\left( {h,k} \right)$ be the coordinates of the vertex of a Parabola and $a$ is the multiplier.
Now, we will write the vertex form for the given equation by using the general vertex form of the Parabola, we get
$\Rightarrow y = {\left( {x - 0} \right)^2} + 6$
So, the vertex of the Parabola $\left( {h,k} \right)$ is $\left( {0,6} \right)$ and the multiplier $a$ is $1$.
Now, we will draw the Parabola with the vertex $\left( {0,6} \right)$.

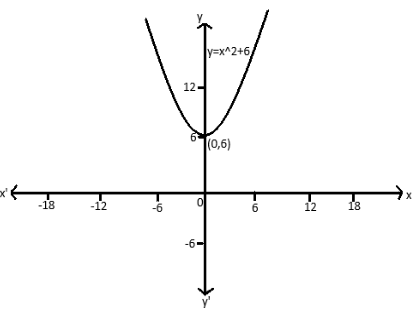
Therefore, the vertex form of the given equation of Parabola $y = {x^2} + 6$ is $y = {\left( {x - 0} \right)^2} + 6$.

Note:
We know that a parabola is symmetric with its axis. If the equation has ${y^2}$ term, then the axis of symmetry is along the x-axis and if the equation has ${x^2}$ term, then the axis of symmetry is along the y-axis. We should know that the vertex of a Parabola is the minimum or maximum point of a Parabola. We will find the type of Parabola, by using the sign of the multiplier $a$ in the vertex form of the parabola. If $a$is positive in $y = a{(x - h)^2} + k$ , then the parabola is open upwards and if $a$ is negative in $y = a{(x - h)^2} + k$ , then the parabola is open downwards. So, the given equation of Parabola is open upwards.