Solveeit Logo
Login

Question

Question: How do you write the point slope form of the equation given (4, 7) and (5, 1)?...

How do you write the point slope form of the equation given (4, 7) and (5, 1)?

Explanation

Solution

This type of question is based on the concept of straight lines. We have to find the equation of the line using the given points. In order to do that, we first find the slope of the line using the given points. Then we use this slope and any one of the given points to find the equation of the line.

Complete step by step answer:
Let us consider the given points that is, (4, 7) and (5, 1). Using these 2 points, we find out the equation in point slope form.
We know that if the points are (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2),\left( {{x}_{2}},{{y}_{2}} \right), then the slope of this line is,
m=y2−y1x2−x1......(1)m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}......(1)
Using this equation (1), we can find the slope of the line as,
⇒m=1−75−4 ⇒m=−61 \begin{aligned} & \Rightarrow m=\dfrac{1-7}{5-4} \\\ & \Rightarrow m=\dfrac{-6}{1} \\\ \end{aligned}
We get the slope as -6.
⇒m=−6\Rightarrow m=-6
Now as we all know, the point slope form is defined as follows.
If the point on a line is (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and the slope of the line is m,m, the point slope form of a line can be written as
y−y1=m(x−x1)......(2)y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)......(2)
Therefore, we can write the equation of the line using any one of the points (4, 7) and (5, 1) and the slope m=−6.m=-6.
Let us use the point (5, 1) here,
⇒y−1=−6(x−5)\Rightarrow y-1=-6\left( x-5 \right)
⇒y−1=−6x+30\Rightarrow y-1=-6x+30
The above equation can also be written as,
⇒y=−6x+30+1 ⇒y=−6x+31......(3) \begin{aligned} & \Rightarrow y=-6x+30+1 \\\ & \Rightarrow y=-6x+31......(3) \\\ \end{aligned}
We can take reference from the following figure which indicates the line y=−6x+31.y=-6x+31.

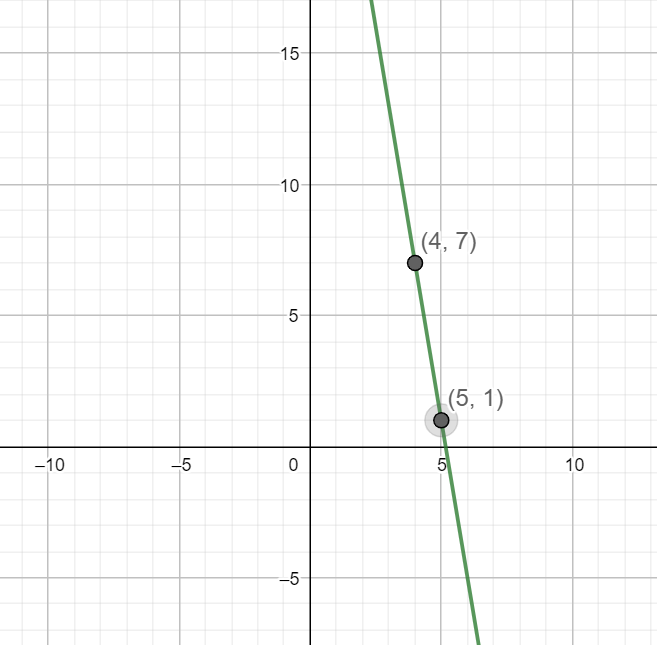
Hence, we have solved the equation to point slope form and this equation is given by y−1=−6(x−5)y-1=-6\left( x-5 \right) and this is simplified to the form y=−6x+31.y=-6x+31.

Note: While solving this question, the students need to have a sound knowledge in straight line topics to easily solve this. While considering the points (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2),\left( {{x}_{2}},{{y}_{2}} \right), we can choose either of the set of points in any order that is (4, 7) and (5, 1) or (5, 1) and (4, 7).