Question

How do you write the following in interval notation: $4 > x\text{ or }3 > x$?

Answer 1

In the above problem, we are asked to write the inequalities $4 > x\text{ or }3 > x$ in interval notation. We know that if we have given $2 > x$ then the interval notation for this inequality is $x\in \left( -\infty ,2 \right)$ so using this notation we can write the interval notation for $4 > x\text{ or }3 > x$. Also, there is a word “or” in this inequality which means we have to take the union of these two inequalities.

Complete step-by-step solution:
The inequalities given in the above problem is as follows:
$4 > x\text{ or }3 > x$
Now, we are going to write the interval notation for $4 > x$ which is equal to:
$x\in \left( -\infty ,4 \right)$
And then, we are going to write the interval notation for $3 > x$ which is equal to:
$x\in \left( -\infty ,3 \right)$
In the above problem, we have given $4 > x\text{ or }3 > x$, the “or” sign means the union of these two inequalities. So, applying the union in the interval notation for $4 > x\text{ or }3 > x$ we get,
$x\in \left( -\infty ,4 \right)\bigcup x\in \left( -\infty ,3 \right)$
Now, finding the union of the above two intervals by plotting these intervals on the number line.

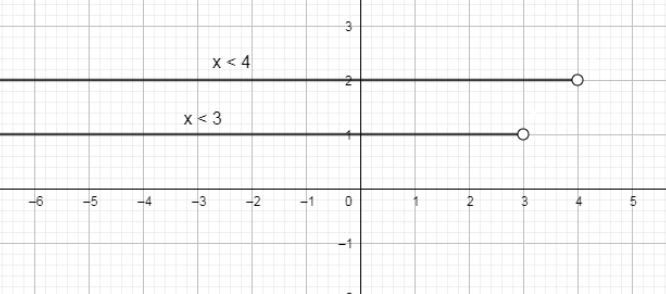
The union of the two intervals is equal to:
$x\in \left( -\infty ,4 \right)$
Hence, the interval notation for the given inequality is $x\in \left( -\infty ,4 \right)$.

Note: In the above problem, if instead of union, intersection will be given and it will look like:
$4 > x\text{ and }3 > x$
“And” is the common region between the two intervals so the interval notation for the above is as follows:
$x\in \left( -\infty ,4 \right)\bigcap x\in \left( -\infty ,3 \right)$
Now, plotting these two intervals on the number line we get,

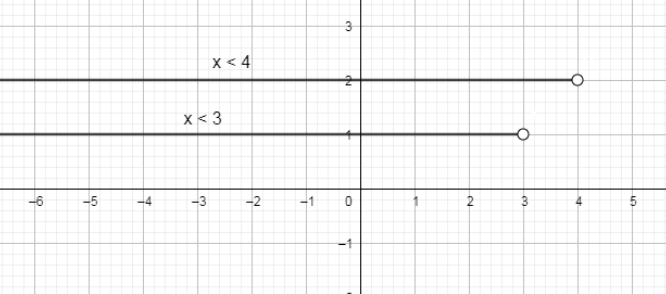
As you can see that the common region is $x<3$ and the interval notation for this inequality we get,
$x\in \left( -\infty ,3 \right)$
The difference between union and the intersection is that in union we will take the largest interval just like we have taken in the above solution as $x\in \left( -\infty ,4 \right)$ and the intersection only involve the common region between the two intervals or you can say the smallest interval i.e. $x\in \left( -\infty ,3 \right)$.