Question

How do you write the equation of the parabola that has the same shape as $y={{x}^{2}}$ but has a vertex of $\left( -3,2 \right)$?

Answer 1

In order to solve the given question, first we need to know that the vertex form of the equation is given by $y=a{{\left( x-p \right)}^{2}}+q$ where $\left( p,q \right)$ is the vertex. Then we draw the graph of the given parabola i.e. $y={{x}^{2}}$, from here we can observed that the vertex of the given graph is at origin and has parameter ‘a’ is equal to 1. Substituting the values we will get the vertex form of the equation of the given graph. Then now it is given in the question the equation of the parabola that has the same shape as $y={{x}^{2}}$ but has a vertex of $\left( -3,2 \right)$, therefore we need to replace the vertex points with $\left( -3,2 \right)$ and the value of ‘a’ remains same. Substituting the values, we will get the required equation of the parabola.

Formula used:
The vertex form of the equation is given by;
$\Rightarrow y=a{{\left( x-p \right)}^{2}}+q$
Where, $\left( p,q \right)$ is the vertex and ‘a’ is the parameter.

Complete step by step answer:
We have given the equation of the parabola i.e.,
$y={{x}^{2}}$
And a vertex that is equal to $\left( -3,2 \right)$.
Now,
As we know that,
The vertex form of the equation is given by;
$\Rightarrow y=a{{\left( x-p \right)}^{2}}+q$
Where, $\left( p,q \right)$ is the vertex.
Now,
Considering the graph of $y={{x}^{2}}$, as shown below.

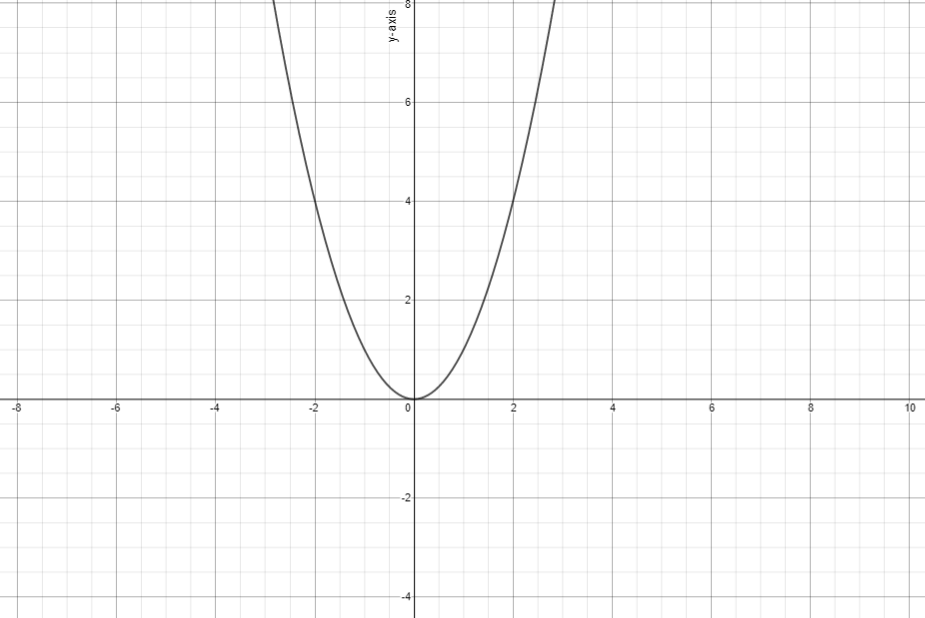
From the graph,
We can observed that the vertex is at origin i.e. $\left( 0,0 \right)$.
Since,
This graph is neither stretched nor compressed.
Therefore,
We can take parameter i.e. $a=1$.
Now,
The equation of the above graph in the vertex form is given by,
$\Rightarrow y=a{{\left( x-p \right)}^{2}}+q$
Where,
$a=1$ and the vertex $\left( p,q \right)=\left( 0,0 \right)$
Therefore,
$\Rightarrow y=1{{\left( x-0 \right)}^{2}}+0$
Now,
In the given question,
It is given that the equation of the parabola that has the same shape as $y={{x}^{2}}$but has a vertex of $\left( -3,2 \right)$.
Therefore,
Here,
$a=1$ and the vertex $\left( p,q \right)=\left( -3,2 \right)$.
Hence,
The vertex form of the equation is given by,
$\Rightarrow y=1{{\left( x-\left( -3 \right) \right)}^{2}}+2$
Simplifying the above equation, we will get
$\Rightarrow y={{\left( x+3 \right)}^{2}}+2$
Therefore,
The equation of the parabola that has the same shape as $y={{x}^{2}}$but has a vertex of $\left( -3,2 \right)$ is $y={{\left( x+3 \right)}^{2}}+2$.
Hence, this is the required answer.

Note: Students need to know about the vertex form of the equation that is given by $y=a{{\left( x-p \right)}^{2}}+q$ where $\left( p,q \right)$ is the vertex. While solving the given question, here we observed that the graph of $y={{x}^{2}}$ is neither stretched nor compressed so that the parameter ‘a’ is equals to 1. Then students need to know that the parameter ‘a’ control the shape of the parabola and in the given question it is given that the parabola has the same shape as of $y={{x}^{2}}$, thus knowing this our new function that we get while solving the question has same parameter.