Question

How do you write the equation of the circle with the given centre and radius: centre at $\left( 3,-6 \right)$ and radius $=5$ ?

Answer 1

In this problem, we can see that the centre of the circle is not at the origin. So, we need to translate the origin to the centre $\left( 3,-6 \right)$ and then write the standard form of the circle using the new coordinates. After that, we convert back to the original coordinates by using the conversion formulae
$\begin{aligned} & X=x-3 \\\ & Y=y+6 \\\ \end{aligned}$

Complete step by step answer:
The circle is a shape, or rather a conic section which has some unique characteristics. The characteristics include that it is the locus of a point with constant distance from a fixed point called the centre. This means that the radius of curvature and the curvature of a circle is constant. The standard equation of a circle is ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ where r is the radius of the circle.
In the standard equation of the circle, it is assumed that the centre of the circle lies at the origin. But, in the problem, the given circle has its centre at $\left( 3,-6 \right)$ , which is clearly not the origin. So, we cannot directly use the standard form here. But we can create a situation to use the standard form by shifting the origin to $\left( 3,-6 \right)$ . For that, we need another set of coordinates, which will be,
$\begin{aligned} & X=x-3 \\\ & Y=y+6 \\\ \end{aligned}$

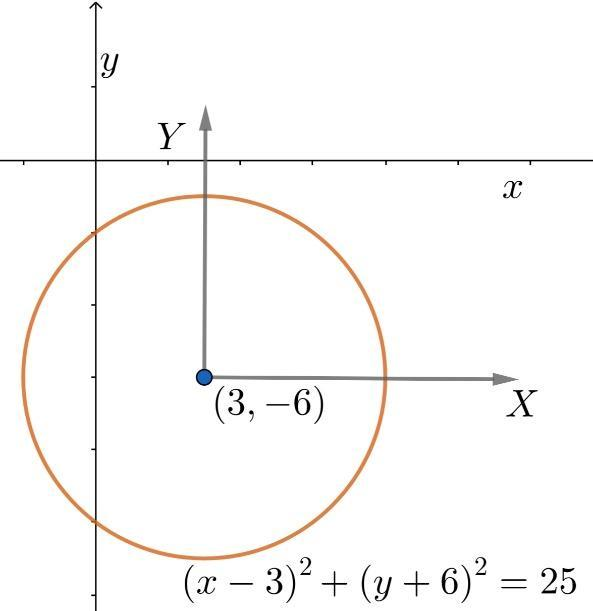
After we have shifted the origin to the centre, we can directly use the standard form, but with variables X and Y instead of x and y. This goes as,
$\begin{aligned} & \Rightarrow {{X}^{2}}+{{Y}^{2}}={{5}^{2}} \\\ & \Rightarrow {{X}^{2}}+{{Y}^{2}}=25 \\\ \end{aligned}$
We now replace X with $x+3$ and Y with $y-6$ in the above equation and get,
$\Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y+6 \right)}^{2}}=25$

Therefore, the equation of the given circle is ${{\left( x-3 \right)}^{2}}+{{\left( y+6 \right)}^{2}}=25$

Note: The problem requires the translation of coordinates which means that we must be very careful while changing the coordinate system and use the proper conversion formulae. This problem can also be solve using a dedicated formula for circle with an offset centre and given radius, which is ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where, $\left( a,b \right)$ is the centre and r is the radius.