Solveeit Logo
Login

Question

Question: How do you write the equation of the circle with Center (3, 4) and radius 6 units?...

How do you write the equation of the circle with Center (3, 4) and radius 6 units?

Explanation

Solution

To find the equation of the circle with center (3, 4) and radius 6 units, we will be using the standard equation of a circle. We know that for a circle with centre (h,k)\left( h,k \right) and radius a units, the equation of the circle is given as (x−h)2+(y−k)2=a2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{a}^{2}} . If we substitute the given centre and radius in the standard equation, we will get the required equation of the circle.

Complete step by step solution:
We need to find the equation of the circle with center (3, 4) and radius 6 units. We know that for a circle with centre (h,k)\left( h,k \right) and radius a units, the equation of the circle is given as
(x−h)2+(y−k)2=a2...(i){{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{a}^{2}}...(i)
We are given the required circle will have a centre of (3, 4) and radius 6 units. When comparing this with the standard form, we will get h=3,k=4h=3,k=4 .
Now, let us write the equation of the required circle in the form given in equation (i). We will be getting
(x−3)2+(y−4)2=62{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}={{6}^{2}}
Let us expand the square terms. We know that (a−b)2=a2−2ab+b2{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}} .
∴(x−3)2+(y−4)2=62 ⇒x2−2x×3+32+y2−2y×4+42=36 \begin{aligned} & \therefore {{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}={{6}^{2}} \\\ & \Rightarrow {{x}^{2}}-2x\times 3+{{3}^{2}}+{{y}^{2}}-2y\times 4+{{4}^{2}}=36 \\\ \end{aligned}
Let us simplify the above equation.
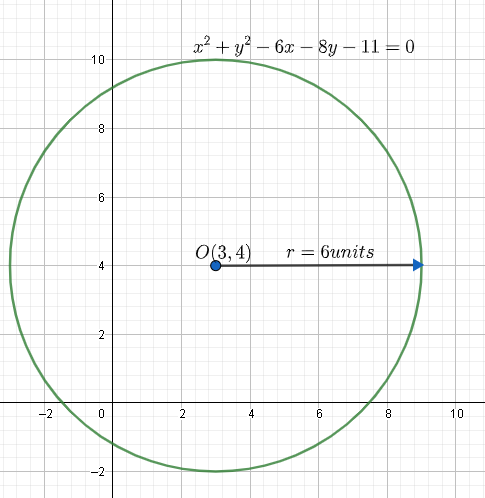
⇒x2−6x+9+y2−8y+16=36 ⇒x2+y2−6x−8y+25=36 ⇒x2+y2−6x−8y+25−36=0 ⇒x2+y2−6x−8y−11=0 \begin{aligned} & \Rightarrow {{x}^{2}}-6x+9+{{y}^{2}}-8y+16=36 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-6x-8y+25=36 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-6x-8y+25-36=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-6x-8y-11=0 \\\ \end{aligned}

We can draw this circle as shown below.

Note: Students have a chance of making mistake by writing the standard equation of the circle as (x−k)2+(y−h)2=a2{{\left( x-k \right)}^{2}}+{{\left( y-h \right)}^{2}}={{a}^{2}} , for a circle of centre (h,k)\left( h,k \right) and radius a units. They may even miss out the square of the radius in the right side of the equation. Students must know the algebraic rules and identities to solve the equation.