Question

How do you write the equation of the circle in standard form? Identify the centre and radius of $4{{x}^{2}}+4{{y}^{2}}+12x-24y+41=0$ ?

Answer 1

We first take an arbitrary point on the x-y plane and equate its distance from the origin with an arbitrary radius r to get the standard form of equation. For the second part, we first divide both sides by $4$ and then compare it with the general form ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ to get the centre $\left( -g,-f \right)$ and radius r in $c={{g}^{2}}+{{f}^{2}}-{{r}^{2}}$ .

Complete step by step answer:
The definition of a circle is that it is a locus of a point which remains at a constant distance from a fixed point. This fixed point is called the centre of the circle. Now, let this fixed point be the origin. Let us take an arbitrary point $\left( x,y \right)$ . The distance of this arbitrary point from the fixed point or the origin will be, $\sqrt{{{x}^{2}}+{{y}^{2}}}$ . This distance will be constant and the value of the constant will be equal to the radius of the circle. In other words, the equation will become,
$\Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=r$
Squaring both sides of the equation, we get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}={{r}^{2}}$
This is the equation of the circle in the standard form.

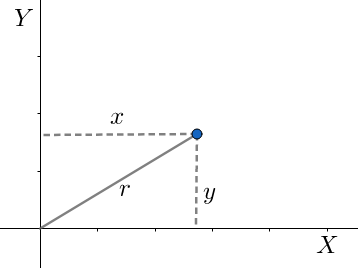
There is another form of equation of circle, which is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ where, the centre of the circle is $\left( -g,-f \right)$ and $c={{g}^{2}}+{{f}^{2}}-{{r}^{2}}$ , r being the radius. The given equation in our problem is,
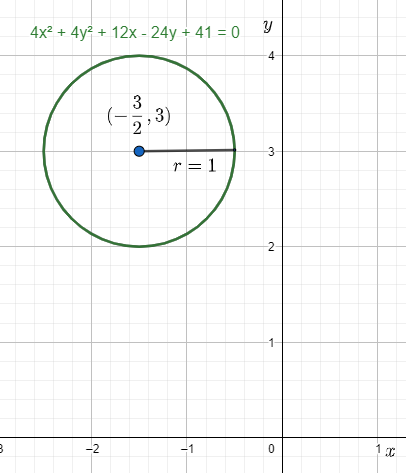
$4{{x}^{2}}+4{{y}^{2}}+12x-24y+41=0$
To make it comparable with the general equation, we divide both sides by $4$ and get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}+3x-6y+\dfrac{41}{4}=0$
Clearly, $g=\dfrac{3}{2},f=-3,c=\dfrac{41}{4}$ . This means,
$\begin{aligned} & \dfrac{41}{4}={{\left( \dfrac{3}{2} \right)}^{2}}+{{\left( -3 \right)}^{2}}-{{r}^{2}} \\\ & \Rightarrow r=\dfrac{9}{4}+9-\dfrac{41}{4} \\\ & \Rightarrow r=\dfrac{4}{4}=1 \\\ \end{aligned}$
Therefore, the radius of the circle is $1$ units and the centre is $\left( -\dfrac{3}{2},3 \right)$ .

Note: This is a very long question, with two parts. So, we must be extra cautious here. Moreover, this problem requires two different forms of the equation of the circle, the standard form and the general form. The second part can also be solved by rearranging the equation as the sum of two squares like ${{\left( x+\dfrac{3}{2} \right)}^{2}}+{{\left( y-3 \right)}^{2}}=1$ from which we can directly get the centre and the radius.