Question

How do you write the equation of a line in slope intercept form, that contains the points $\left( -8,2 \right)$ and $\left( 3,2 \right)$ ?

Answer 1

The first thing that we have to do in this problem is to incorporate the two-point method as we are given two points that lie on the line. We put the points in the equation $y-{{y}_{1}}=\left( {{y}_{2}}-{{y}_{1}} \right)\times \dfrac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and then simplify and rearrange to make it of the slope-intercept form $y=mx+c$ .

Complete step by step answer:
A straight-line equation can be expressed in several ways or forms such as the slope intercept form, the intercept form, the two-point form and so on. Each of these forms has their own applications and times of use. The slope intercept form is used when the slope and y-intercept of the line are known, the intercept form is used when both the x and the y intercepts are known and the two-point form is preferable when we are given two such points that lie on the line.
As in this problem, we are given two points that lie on the line, we should use the two-point form. The form is,
$y-{{y}_{1}}=\left( {{y}_{2}}-{{y}_{1}} \right)\times \dfrac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Where, $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the two given points on the line. Here, $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are $\left( -8,2 \right)$ and $\left( 3,2 \right)$ respectively. So, putting these values in the two-point form, we get,
$\Rightarrow y-2=\left( 2-2 \right)\times \dfrac{x-\left( -8 \right)}{3-\left( -8 \right)}$
Carrying out the requires arithmetic operations in the above equation, we get,
$\begin{aligned} & \Rightarrow y-2=0 \\\ & \Rightarrow y=2 \\\ \end{aligned}$
The final equation is even in the slope-intercept form as it is of the form $y=mx+c$ and here, $m=0$ and $c=2$ .
Therefore, we can conclude that the slope-intercept form for the given straight-line is $y=2$ .

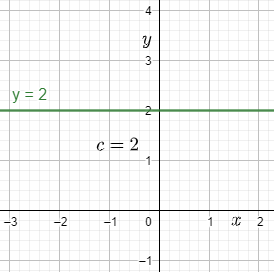
Note: The problem is a bit tricky as it demands one form and requires the use of another. So, we must be wise enough to choose which form to use and when. Also, the problem can be solved using a simple analysis of the line. We can see that the ordinates of the two points are the same, which is $2$ . That means, the ordinate or y is constant over here and the constant is $2$ . Also, ordinate constant means a line parallel to the x-axis and thus having slope zero.