Question

How do you write the equation of a line going through (d,0) and parallel to $y=mx+c$ ?

Answer 1

First we have to find the slope of the required line by using the standard slope-intercept form which is given as $y=mx+c$ . We know that when a line is parallel to another line, their slopes will be equal. Hence, the slope of the required line will be m. Now, we have to use the point-slope formula, that is, $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ , and substitute the values to get the required answer.

Complete step by step answer:
To get the equation of a line passing through the point (d,0) and parallel to $y=mx+c$ , we will first find the slope of the line from the equation $y=mx+c$ . Here, m is the slope and c is the y-intercept.
We know that when a line is parallel to another line, their slopes will be equal. Hence, the slope of the required line will be m.
Now, we have to use the point-slope formula to find the equation of the required line. We can write the point-slope formula as
$\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ , where m is the slope and $\left( {{x}_{1}},{{y}_{1}} \right)$ denotes the point through which the line passes.
Now, we have to substitute the values in the above formula. Here, the slope is $m$, which is the slope of the required line, and the point is (d, 0) . We will get
$\left( y-0 \right)=m\left( x-d \right)$
$\Rightarrow y=mx-md$
We can represent this problem in the graph below. We can draw the graph with the given points and equations by setting $d=1,m=1\text{ and }c=1$ .

Hence, the answer is $y=mx-md$ .

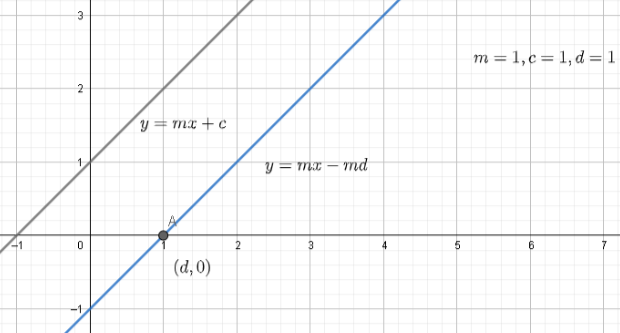
Note: Students may make mistakes by writing $y=mc+x$ instead of $y=mx+c$ . They may misunderstand the slope of parallel lines to be ${{m}_{p}}=-\dfrac{1}{m}$ . The equation $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ can be misunderstood as $\left( x-{{x}_{1}} \right)=m\left( y-{{y}_{1}} \right)$.