Question

How‌ ‌do‌ ‌you‌ ‌write‌ ‌the‌ ‌equation‌ ‌of‌ ‌a‌ ‌line‌ ‌with‌ ‌slope‌ ‌$1$‌ ‌and‌ ‌y-intercept‌ ‌$4$?‌ ‌

Answer 1

In order to find the solution of the given question that is to write the equation of a line with slope $1$ and y-intercept $4$ use the standard equation of straight-line $y=mx+c$ where $m$ is the slope of the line and $c$ is the intercept of the straight line. As here, we have the value of slope and y-intercept then we can put these values in the standard equation to find the required equation.

Complete step-by-step solution:
According to the question,
Given slope in the question is $1$ and the value of y-intercept is $4$,
We know that the standard equation of straight line is $y=mx+c$ or we can say $y=\text{slope}\times x+y\text{-intercept}$
Now, substituting the given values in the above formula we will have:
$\Rightarrow y=\left( 1 \right)x+4$
After solving the bracket, we get:
$\Rightarrow y=x+4$
Let’s draw the graph and point out the y-intercept.

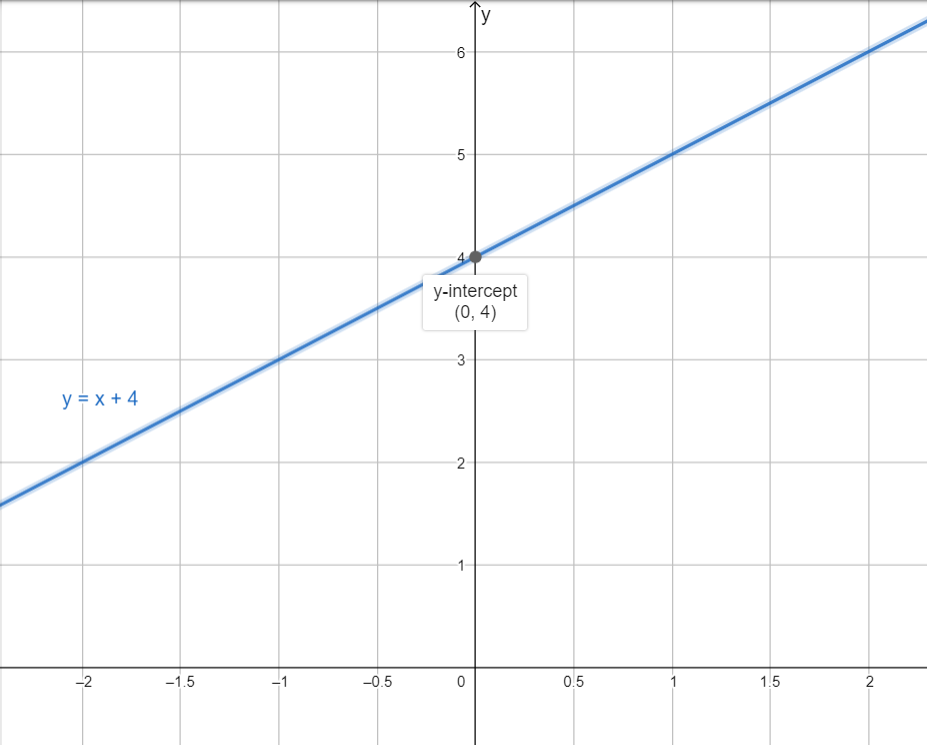
We can see in the above figure that the straight line is $y=x+4$ and the y-intercept is at the point $\left( 0,4 \right)$.
Therefore, the equation of straight line with slope as $1$ and y-intercept as $4$ is $y=x+4$.

Note: There’s an alternative method to find the equation of the straight line.
As we know that y-intercept is $4$, so the straight line will pass through the point $\left( 0,4 \right)$ and the slope of this line is $1$.
Let the point $\left( x,y \right)$ lie on the straight line so the value of slope will be $\dfrac{y-4}{x-0}$ will be equal to $1$.
We can rewrite the above statement as follows:
$\Rightarrow \dfrac{y-4}{x-0}=1$
$\Rightarrow \dfrac{y-4}{x}=1$
Simplifying it further by cross multiplying the above equation, we will have:
$\Rightarrow y-4=x$
$\Rightarrow y=x+4$
Therefore, the equation of straight line with slope as $1$ and y-intercept as $4$ is $y=x+4$.