Question

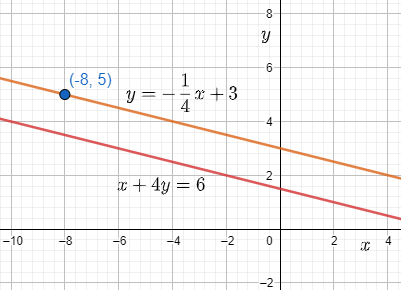
How do you write the equation in slope-intercept form parallel to the line $x+4y=6$ and passes through $\left( -8,5 \right)$ ?

Answer 1

At first, we rearrange the given equation in the slope-intercept form to $y=-\dfrac{1}{4}x+\dfrac{3}{2}$ in order to get its slope which is $-\dfrac{1}{4}$ . Since, the required line is parallel to it, it must also have slope $-\dfrac{1}{4}$ and some y-intercept c, which will be found out by putting the point $\left( -8,5 \right)$ in the equation $y=-\dfrac{1}{4}x+c$ .

Complete step by step answer:
A straight-line equation can be expressed in several ways or forms such as the slope intercept form, the intercept form, the two-point form and so on. Each of these forms has their own applications and times of use. The slope intercept form is used when the slope and y-intercept of the line are known, the intercept form is used when both the x and the y intercepts are known and the two-point form is preferable when we are given two such points that lie on the line.
We rearrange the given line in the slope-intercept form $y=mx+c$ . This goes as,
$\begin{aligned} & \Rightarrow 4y=-x+6 \\\ & \Rightarrow y=-\dfrac{1}{4}x+\dfrac{3}{2} \\\ \end{aligned}$
The slope of the given line is clearly $-\dfrac{1}{4}$ . So, any line parallel to it has the same slope $-\dfrac{1}{4}$ . Writing the equation of the required line in the slope intercept form with slope $m=-\dfrac{1}{4}$ and an arbitrary y-intercept c, we get
$y=-\dfrac{1}{4}x+c$
But the above line passes through the point $\left( -8,5 \right)$ . So, putting the point in the above equation, we get,
$\begin{aligned} & \Rightarrow 5=-\dfrac{1}{4}\left( -8 \right)+c \\\ & \Rightarrow c=3 \\\ \end{aligned}$
Therefore, we can conclude that the equation of the required line is $y=-\dfrac{1}{4}x+3$ .

Note: While solving these types of problems, we should carefully see whether the question says “parallel” or “perpendicular”, which if overlooked can lead to wrong answers. The problem can also be solved by the point-slope formula which is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the point on it and m is its slope.